TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

A dispersão de Rayleigh (em homenagem a Lord Rayleigh) é a dispersão da luz ou qualquer outra radiação eletromagnética por partículas muito menores que o comprimento de onda dos fótons dispersados. Ocorre quando a luz viaja por sólidos e líquidos transparentes, mas se observa com maior frequência nos gases. A dispersão de Rayleigh da luz solar na atmosfera é a principal razão pela qual o céu é azul.

Se o tamanho das partículas é maior que o comprimento de onda, a luz não se decompõe em suas componentes cromáticas e todos os comprimentos de onda são igualmente dispersados, motivo pelo qual, ao atravessar uma nuvem, esta se vê como branca; o mesmo ocorrendo quando atravessa os grãos de sal e de açúcar. Para que a luz seja dispersada, o tamanho das partículas deve ser similar ou menor que o comprimento de onda.

O grau de dispersão de Rayleigh que sofre um raio de luz depende do tamanho das partículas e do comprimento de onda da luz, dependências expressas de fato no coeficiente de dispersão; a intensidade da luz dispersada depende inversamente da quarta potência do comprimento de onda, relação conhecida como Lei de Rayleigh-Jeans. A dispersão de luz por partículas maiores a um décimo do comprimento de onda se explica com a teoria de Mie, que é uma explicação mais geral da difusão de radiação electromagnética.

Índice

• 1Equacionamento
• 2Por que o céu é azul?
  • 2.1E de fora do planeta, enxergamos a Terra de que cor?
• 3Observações
• 4Ver também
• 5Referências
• 6Bibliografia
• 7Ligações externas

Equacionamento

A intensidade I da luz dispersada por uma pequena partícula num feixe de luz de comprimento de onda λ e intensidade I₀ é dada por:

${\displaystyle I=I_{0}\,{\frac {1+\cos ^{2}\theta }{2\,R^{2}}}\left({\frac {2\pi }{\lambda }}\right)^{4}\left({\frac {n^{2}-1}{n^{2}+2}}\right)^{2}\left({\frac {d}{2}}\right)^{6}}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Onde R é a distância à partícula, θ é o ângulo de dispersão, n é o índice de refração da partícula e d é o diâmetro da partícula.

No caso de luz polarizada (e não se pode generalizar) também podemos expressar:

${\displaystyle I=I_{0}\,|\sigma (\theta ,\phi )|^{2}\,{\frac {(2\pi )^{2}}{(\lambda R)^{2}}}}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

${\displaystyle \sigma (\theta ,\phi )=A(\theta )\operatorname {sen} {\phi }\,{\hat {e}}_{\phi }+B(\theta )\cos {\phi }\,{\hat {e}}_{\theta }}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Onde agora a parte dos símbolos anteriores temos o coeficiente de dispersão σ, e os ângulos em coordenadas esféricas θ e Φ. Onde seus vetores unitários se definem referidos ao plano que definem o vetor que contém a direção de propagação da radiação e o vetor que contém a direção da polarização da onda incidente. A parte temos os coeficientes da matriz de Lennard-Jones perpendicular A(θ) e paralelo B(θ) ao plano de dispersão.

A distribuição angular da dispersão de Rayleigh, que vem a ser dada pela fórmula (1+cos²θ), é simétrica no plano perpendicular à direção da luz incidente, portanto a luz dispersada iguala-se à luz incidente. Integrando a área da esfera que cerca una partícula obtemos a seção de choque da dispersão de Rayleigh, σ_s:

${\displaystyle \sigma _{s}={\frac {2\pi ^{5}}{3}}{\frac {d^{6}}{\lambda ^{4}}}\left({\frac {n^{2}-1}{n^{2}+2}}\right)^{2}}$

O coeficiente de dispersão para um grupo de partículas é o número de partículas por unidade de volume N vezes a seção transversal. Como em todos os efeitos de onda, na dispersão incoerente as potências são somadas aritmeticamente, ainda que na dispersão coerente (como acontece quando as partículas estão muito próximas umas das outras) os campos são somados aritmeticamente e a soma deve ser elevada ao quadrado, para obter a potência final.

Por que o céu é azul?

Observe o intervalo de comprimentos de onda que o ser humano pode enxergar através do olho.

Gráfico que mostra a comparação das cores às quais os nossos olhos tem maior sensibilidade quando sob efeito do espalhamento. Note que o olho humano é muito mais sensível ao azul do que ao verde e ao vermelho.^[1]

Primeiramente, deve-se salientar que a explicação para esse fenômeno envolve muitos conhecimentos especializados, tais como, a fisiologia do olho humano, a nossa percepção às cores, bem como o processo físico que tem o nome de “espalhamento”. Como as cores que enxergamos fazem parte de uma pequena parcela do espectro eletromagnético, a qual compreende os tamanhos de, aproximadamente, 380 a 720 nm de comprimento de onda (violeta a vermelho, respectivamente), existem algumas que são mais espalhadas do que outras, o que podemos concluir apenas observando a equação mostrada anteriormente: a intensidade da luz varia com λ⁻⁴, ou seja, para comprimentos de onda pequenos, como é o caso do violeta (~400 nm) e azul (~450 nm), há um maior espalhamento em relação ao resto da luz visível, ainda sendo o do violeta maior que o do azul. Nesse momento, surge a dúvida "mas por que enxergarmos o céu com coloração azul se há, de fato, um maior espalhamento de ondas de cor violeta?". Isso se explica pelos outros dois fatores salientados anteriormente: a fisiologia do olho humano e a nossa percepção às cores. O conjunto olho humano-cérebro é o responsável por enxergarmos a coloração azulada, pois no olho existem células chamadas "cones", que nos dão a possibilidade de percepção das diferentes cores, e são muito mais sensíveis ao vermelho, verde e, principalmente, ao azul. Por causa dessa característica, é possível entender o porquê de enxergarmos o céu com a coloração azulada, ao invés da roxa. O céu de outros planetas também sofre o efeito do espalhamento. Marte, por exemplo, tem o céu variando desde a cor cinza até rosa alaranjada, devido ao fato de a atmosfera marciana ser muito rarefeita e empoeirada. Isso foi confirmado pelos módulos de pouso das sondas espaciais, norte-americanas, Viking nos anos de 1970 e pelos “rovers” (pequenos carrinhos) norte-americanos Spirit e Opportunity em 2004. O espalhamento de luz atmosférica é dominado não pelas moléculas de gás (no caso de Marte a maior parte delas é dióxido de carbono), mas por partículas de poeira que estão em suspensão. Essas partículas são maiores do que os comprimentos de onda da luz visível e elas são avermelhadas, pelo óxido de ferro, como o solo marciano. Não é apenas espalhamento Rayleigh, de modo que o espectro de potência é diferente.

E de fora do planeta, enxergamos a Terra de que cor?

O primeiro ser humano a ir ao espaço foi o russo Yuri Gagarin e isso aconteceu no dia 12 de abril de 1961. Gagarin permaneceu 1 hora e 48 minutos circulando em torno da Terra a bordo de uma pequena cápsula chamada Vostok 1, a uma altitude de máxima de 327,7 quilômetros. Olhando a Terra a partir do espaço Gagarin disse uma frase que ficou célebre: “A Terra é azul”. Essa resposta, entretanto, não é óbvia, visto que a origem dessa cor é bem diferente da cor azul que vemos quando estamos no solo terrestre. O efeito dominante que faz com que, do espaço, vejamos nosso planeta azul é a maior absorção de longos comprimentos de onda pelos oceanos terrestres, fazendo com que os as ondas de menores comprimentos, principalmente aquelas que correspondem ao azul, sejam refletidas até os olhos de quem observa o planeta do espaço. São os oceanos terrestres (71% da superfície da Terra é coberta por superfícies líquidas) que dão a ela a cor azul, quando é vista por alguém que está no espaço.^[2]

O espalhamento dinâmico de luz (em inglês DLS, Dynamic Light Scattering) é uma técnica de caracterização físico-química que mede a distribuição do tamanho de pequenas partículas e moléculas em solução líquida, sendo preciso e rápido para medir a distribuição de tamanho de partículas com mesmo tamanho, mas não sendo tão preciso com diferenças de tamanho muito grandes.

Do DLS temos a luz se espalhando do material analisado com intensidades diferentes e assim obtemos a distribuição da intensidade pelo tamanho de partícula, e dela podemos obter a distribuição de volume e de quantidade pelo tamanho de partícula pela teoria de Mie.

O DLS é muito importante para a caracterização do tamanho hidrodinâmico de nanopartículas em fluidos biológicos como plasma e diferentes pHs fisiológicos.

Índice

• 1O aparelho
• 2Teoria
• 3Cálculos
• 4Limitações
• 5Referências
• 6Ligações externas

O aparelho

Esquema do funcionamento do DLS

A luz do laser passa por um polarizador e atinge uma cubeta com o material desejado. A luz espalhada do material passa por um analisador que seleciona uma determinada polarização e entra no detector, cuja posição define o ângulo de espalhamento e o volume de espalhamento de uma região.

O DLS possui um correlator que mede o grau de semelhança entre dois sinais de intensidade em diferentes tempos, e calculando a função de correlação da luz espalhada temos o coeficiente de difusão e dele obtemos o tamanho médio de partícula.

Teoria

A estrutura de complexos moleculares é conhecida em razão da absorção da radiação eletromagnética, que fornece informações sobre o nível de energia translacional, rotacional, vibracional e eletrônico das moléculas. As mudanças de frequência, distribuição angular, polarização e intensidade da luz espalhada são determinadas pelo tamanho, forma e interações moleculares do material. E com o uso do laser pode-se medir variações de frequências bem pequenas do espalhamento de luz da amostra e também fracos espalhamentos de luz por causa da alta intensidade do laser, permitindo a medida de nanômetros.

Correlação com a intensidade

A intensidade espalhada é medida baseada na dispersão de Rayleigh, por um contador de fótons e está ligada à difusão da molécula no solvente, com as pequenas partículas se movendo mais rápido do que as grandes, tendo maior variação.

As partículas suspendidas no solvente líquido se movem com o tempo de acordo com o movimento browniano, com a luz espalhada de duas ou mais moléculas tendo interferências construtivas ou destrutivas variando com o tempo e gerando alterações na intensidade da luz dispersada se a molécula não for menor do que o comprimento de onda.

Ao ser atingido pela luz, os elétrons do material sofrem uma polarização oscilante em função do campo elétrico da luz e quando o dipolo muda, a energia é irradiada e com isso ele passa a ser uma fonte secundária de luz, espalhando luz em todas as direções.

O tamanho de partículas adquirido é o diâmetro hidrodinâmico, que varia dependendo da força iônica e da estrutura superficial. Uma baixa concentração iônica terá a camada de íons estendida ao redor da partícula, diminuindo a velocidade de difusão e aparentando um diâmetro hidrodinâmico maior, enquanto em altas concentrações a camada será comprimida e a mesma partícula apresentará menor diâmetro hidrodinâmico. Quanto à superfície, uma camada adsorvida pela partícula pode ter sua conformação alterada dependendo do meio aquoso e da própria superfície da partícula. Quando a partícula não é esférica, o valor obtido é de uma esfera com o mesmo coeficiente de difusão translacional.

Cálculos

Devido ao índice de refração, a variação da intensidade da luz pode ser calculada usando a função de correlação cruzada das intensidades normalizada de segunda ordem:

g₂(τ) = G₂(τ)÷${\displaystyle I^{2}}$, que também pode ser descrito como I(t)I(t+τ) = ${\displaystyle \lim _{N\to \infty }{\frac {1}{N}}\sum _{j}^{N}I(j)I(j+n)}$ ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

• I é a intensidade média;
• τ é a correlação do tempo;
• G₂(τ) é a função de correlação do tempo.

Da função de correlação de primeira ordem temos: g₁(τ) = e^-q2Dτ

• q é o vetor de espalhamento;
• D é o coeficiente de difusão translacional;
• Γ=-q²×D é a taxa de decaimento.

Vetor de espalhamento (q)

O vetor de espalhamento pode ser obtido por: q = 4πnsen(θ÷2)÷λ

• n o índice de refração da solução;
• λ o comprimento de onda da luz incidente no vácuo;
• θ o ângulo de espalhamento da luz.

O tamanho das partículas em solução é obtido pela equação Stokes-Einstein: D = kT÷(3πηR_h)

• k é a constante de Boltzmann;
• T é a temperatura;
• η é a viscosidade do solvente;
• R_h é o raio hidrodinâmico das partículas em solução.

Na maioria das análises há partículas com tamanhos variados e com isso diferentes taxas Γ distribuídas segundo uma função p(Γ) do sistema, que está relacionado com a relação de primeira ordem: g₁(τ)Γ = ${\displaystyle \int }$₀^∞e^-Γτp(Γ)dΓ

• p(Γ)dΓ é o numero de partículas com valores de gama entre Γ e Γ+dΓ.

A distribuição do tamanho de partículas em dispersão nesse caso pode ser estimada pelo:

1. Método da expansão em cumulantes
2. Método CONTIN
3. Ajuste por multiexponenciais

Intensidade de um feixe gaussiano em torno do foco em um dado instante de tempo, mostrando dois picos de intensidade para cada frente de onda.

Topo: perfil de intensidade transversal de um feixe gaussiano que propaga para fora da página. Curva azul: amplitude do campo elétrico (ou magnético) vs posição radial em relação ao eixo do feixe. A curva preta é a intensidade correspondente.

Perfil de feixe de um apontador laser verde de 5 mW, mostrando o perfil TEM₀₀.

Em óptica, um feixe gaussiano ou feixe de Gauss é um feixe de radiação eletromagnética monocromática, cujos perfis transversais de amplitude do campo elétrico e magnético são dados por uma função de Gauss; isto também implica um perfil de intensidade gaussiano. Este modo gaussiano transversal fundamental (ou TEM₀₀) descreve a saída da maioria (mas não todos) dos lasers, como tal um feixe pode ser focado na região mais concentrada. Quando tal feixe é refocado por uma lente, a dependência de fase transversal é alterada; isto resulta em um feixe gaussiano diferente. Os perfis de amplitude dos campos elétricos e magnéticos em torno de qualquer feixe gaussiano circular (para dado comprimento de onda e polarização) são determinados por um único parâmetro, a chamada cintura do feixe w₀. Em qualquer posição z relativa à cintura (foco) ao longo de um feixe que tem uma w₀ específica, as amplitudes e fases do campo são determinadas^[1] como detalhado abaixo.

Soluções arbitrárias da equação paraxial de Helmholtz podem ser expressas como combinações dos modos de Hermite-Gauss (cujos perfis de amplitude são separados em x e y utilizando coordenadas cartesianas) ou similarmente como combinações dos modos de Laguerre-Gauss (cujos perfis de amplitude são separados em r e θ utilizando coordenadas cilíndricas).^[2][3] Em qualquer ponto ao longo do feixe z, estes modos incluem o mesmo fator de Gauss como o modo gaussiano fundamental multiplicando os fatores geométricos adicionais para o modo específico. Entretanto diferentes modos propagam com uma fase diferente de Gouy, razão pela qual o perfil transversal líquido devido a uma superposição de modos evolui em z, enquanto a propagação de qualquer modo de Hermite-Gauss único retém a mesma forma ao longo do feixe.

Embora existem outras possíveis decomposições modais, estas famílias de soluções são as mais úteis para problemas envolvendo feixes compactos, isto é, quando a potência óptica é bem proximamente confinada ao longo de um eixo. Mesmo quando um laser não está operando em um modo gaussiano fundamental, sua potência irá geralmente ser encontrada nos modos de ordem mais baixa usando estas decomposições, pois a extensão espacial dos modos de ordem mais alta irão tender a exceder as fronteiras de um ressonador (cavidade) laser. "Feixe gaussiano" normalmente implica radiação confinada ao modo gaussiano transversal fundamental (TEM₀₀).

Índice

• 1Forma matemática
  • 1.1Evolução da largura do feixe
  • 1.2Evolução do raio de curvatura
  • 1.3Fase de Gouy
• 2 Parâmetros do feixe
  • 2.1Cintura do feixe
  • 2.2Intervalo de Rayleigh e parâmetro confocal
  • 2.3Divergência do feixe
• 3Potência e intensidade
  • 3.1Potência através de uma abertura
  • 3.2Intensidade de pico
• 4Parâmetros complexos do feixe
• 5Equação da onda
  • 5.1Solução no modo gaussiano
  • 5.2Outras soluções
• 6Modos de ordem superior
  • 6.1Modos de Hermite-Gauss
  • 6.2 Modos de Laguerre-Gauss
  • 6.3 Modos de Ince-Gauss
  • 6.4 Modos Hipergeométrico-Gauss
• 7Ver também
• 8Notas
• 9Referências
• 10Bibliografia
• 11Ligações externas
• 12Notas

Forma matemática

O feixe gaussiano é um modo eletromagnético transversal (TEM). A expressão matemática para a amplitude do campo elétrico é uma solução da equação paraxial de Helmholtz. Assumindo polarização na direção x e propagação na direção +z, a notação do campo elétrico em fasor é dada por:

${\displaystyle {\mathbf {E} (r,z)}=E_{0}\,{\hat {x}}\,{\frac {w_{0}}{w(z)}}\exp \!\left(\!{\frac {-r^{2}}{w(z)^{2}}}\right)\exp \!\!\left(\!\!-i\!\left(kz+k{\frac {r^{2}}{2R(z)}}-\psi (z)\!\right)\!\!\right)\ ,}$ ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde:

${\displaystyle r}$ é a distância radial a partir do eixo central do feixe,

${\displaystyle z}$ é a distância axial a partir do foco do feixe (ou "cintura" do feixe),

${\displaystyle i}$ é a unidade imaginária,

${\displaystyle k=2\pi /\lambda }$ é o número de onda (em radianos por metro) para um comprimento de onda λ,

${\displaystyle E_{0}=E(0,0)}$, a amplitude do campo elétrico (e fase) na origem no tempo 0,

${\displaystyle w(z)}$ é o raio no qual as amplitudes caem a 1/e de seu valor axial, no plano z ao longo do feixe,

${\displaystyle w_{0}=w(0)}$ é o tamanho da cintura,

${\displaystyle R(z)}$ é o raio de curvatura da frente de onda do feixe em z, e

${\displaystyle \psi (z)}$ é a fase de Gouy em z, um termo de fase adicional além daquele atribuível à velocidade de fase da luz.

Há também uma dependência de tempo compreendido ${\displaystyle e^{i\omega t}}$ multiplicando tais quantidades de fasor; o campo real em um ponto no tempo e no espaço é dado pela parte real desta quantidade complexa.

O campo magnético da onda tem uma forma idêntica mas com uma polarização ortogonal (em y uma vez que a polarização do campo elétrico foi estipulada para estar em x):

${\displaystyle {\mathbf {H} (r,z)}={\hat {y}}{\frac {1}{\eta }}{E_{x}(r,z)}}$ ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde a constante η é a impedância característica do meio no qual o feixe está se propagando. Para o espaço livre, η = η₀ ≈ 377 Ω.

A intensidade em média de tempo (ou irradiância) em uma localização é computada utilizando ${\displaystyle I={\frac {1}{2}}\mathbf {Re} (E\times H^{*})}$ a qual remove todos fatores de fase (uma vez que foi feita uma média ao longo do tempo, o que resulta também no fator ½):

${\displaystyle I(r,z)={|E(r,z)|^{2} \over 2\eta }=I_{0}\left({\frac {w_{0}}{w(z)}}\right)^{2}\exp \left({\frac {-2r^{2}}{w^{2}(z)}}\right)\ ,}$ ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde ${\displaystyle I_{0}=E_{0}^{2}/2\eta }$ é a intensidade no centro do feixe em sua cintura.

Evolução da largura do feixe

Em uma posição z ao longo do feixe (medido a partir do foco), o parâmetro tamanho da cintura w é dado por^[4]

${\displaystyle w(z)=w_{0}\,{\sqrt {1+{\left({\frac {z}{z_{\mathrm {R} }}}\right)}^{2}}}\ .}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde^[4]

${\displaystyle z_{\mathrm {R} }={\frac {\pi w_{0}^{2}}{\lambda }}}$

é chamado de intervalo de Rayleigh como discutido mais adiante.

Evolução do raio de curvatura

A curvatura da frente de onda é zero na cintura do feixe e também se aproxima de zero quando z → ±∞. Ela é igual a 1/R onde R(z) é o raio de curvatura como função da posição ao longo do feixe, dado por^[5]

${\displaystyle R(z)=z\left[{1+{\left({\frac {z_{\mathrm {R} }}{z}}\right)}^{2}}\right]\ .}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Fase de Gouy

A chamada fase de Gouy de um feixe em z é dado por:^[5]

${\displaystyle \psi (z)=\arctan \left({\frac {z}{z_{\mathrm {R} }}}\right)\ .}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Esta mudança de fase ao longo do feixe permanece dentro do intervalo ±π/2 (para um feixe gaussiano fundamental) e não é observável em muitos experimentos. Entretanto ela tem importância teórica e assume uma maior gama em modos gaussianos de ordem superior.^[6]

 Parâmetros do feixe

A dependência geométrica dos campos de um feixe gaussiano são governados pelo comprimento de onda da luz λ (no meio dielétrico, se não espaço livre) e os seguintes parâmetros do feixe, todos os quais estão conectados como detalhado nas seções seguintes.

Cintura do feixe

Ver também: Diâmetro do feixe

Largura do feixe gaussiano w(z) como função da distância z ao longo do feixe. w₀: cintura do feixe; b: profundidade de foco; z_R: intervalo de Rayleigh; ${\displaystyle \Theta }$: espalhamento angular total

A forma de um feixe gaussiano de um dado comprimento de onda λ é governado exclusivamente por um parâmetro, a cintura do feixe w₀. Esta é uma medida do tamanho do feixe no ponto de seu foco (z=0 nas equações acima) onde a largura do feixe w(z) (como definido acima) é a menor e da mesma forma onde a intensidade no eixo (r=0) é a maior. A partir deste parâmetro, os outros parâmetros que descrevem a geometria do feixe são determinados. Isto inclui o intervalo de Rayleigh z_R e a divergência assintótica do feixe θ, como detalhado abaixo.

Intervalo de Rayleigh e parâmetro confocal

O intervalo ou comprimento de Rayleigh z_R é determinado dado um tamanho à cintura do feixe gaussiano:

${\displaystyle z_{\mathrm {R} }={\frac {\pi w_{0}^{2}}{\lambda }}}$ .

A uma distância da cintura igual ao intervalo de Rayleigh z_R, a largura w do feixe é ${\displaystyle {\sqrt {2}}}$ mais larga do que ela é no foco, onde w = w₀. Isto também implica que a intensidade deste ponto no eixo (r=0) é metade da intensidade de pico (em z=0). Este ponto ao longo do feixe também é onde a curvatura da frente de onda é a maior (1/R).^[7]

A distância entre os dois pontos z = ±z_R é chamado de parâmetro confocal ou profundidade de foco^{[carece de fontes]} do feixe.

Divergência do feixe

Embora a calda de uma função de Gauss nunca realmente atinja zero, o propósito da seguinte discussão, nos deixa chamar a "borda" de um feixe o raio onde r = w(z). Isto é onde a intensidade é reduzida a 1/e² de seu valor no eixo. Agora, para ${\displaystyle z\gg z_{\mathrm {R} }}$ o parâmetro ${\displaystyle w(z)}$ aumenta linearmente com ${\displaystyle z}$. Isto significa que longe da cintura, o "borda" do feixe tem formato de cone. O ângulo entre linhas ao longo deste cone (cujo ${\displaystyle r=w(z)}$) e o eixo central do feixe (${\displaystyle r=0}$) é chamado de divergência do feixe. Ele é dado por^[7]

${\displaystyle \theta \simeq {\frac {\lambda }{\pi w_{0}}}\qquad (\theta \mathrm {\ em\ radianos} ).}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

O espalhamento angular total do feixe distante da cintura é então dado por

${\displaystyle \Theta =2\theta \ .}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Pelo fato da divergência ser inversamente proporcional ao tamanho da cintura, para um dado comprimento de onda λ, um feixe gaussiano que é focado em uma área pequena diverge rapidamente quando se propaga para longe do foco. Em contrapartida, para minimizar a divergência de um feixe laser no campo distante (e aumentar sua intensidade de pico em distâncias maiores) ele deve ter uma seção transversal grande (w₀) na cintura (e assim um grande diâmetro onde é lançado, de forma que w(z) nunca seja inferior a w₀). Esta relação entre a largura do feixe e divergência é um característica fundamental da difração, e da transformada de Fourier que descreve a difração de Fraunhofer. Um feixe com qualquer perfil de amplitude especificado também obedece esta relação inversa, mas o modo gaussiano fundamental é um caso especial onde o produto do tamanho do feixe no foco e a divergência no campo distante é menor que para qualquer outro caso.

Uma vez que o modelo do feixe gaussiano utiliza a aproximação paraxial, ele falha quando as frentes de onda são inclinadas em mais de aproximadamente 30° do eixo do feixe.^[8] Da expressão acima para divergência isto significa que o modelo do feixe gaussiano é acurado apenas para feixes com cinturas maiores que aproximadamente ${\displaystyle 2\lambda /\pi }$.

A qualidade do feixe laser é quantificado pelo produto do parâmetro do feixe (BPP). Para um feixe gaussiano, o BPP é o produto da divergência do feixe e o tamanho da cintura ${\displaystyle w_{0}}$. O BPP de um feixe real é obtido pela medição do diâmetro mínimo do feixe e da divergência em campo distante, e calculado seu produto. A razao entre o BPP de um feixe real pelo correspondente de um feixe gaussiano ideal no mesmo comprimento de onda é conhecido como M² ("M ao quadrado"). O M² para um feixe gaussiano é um. Todos feixes de laser reais possui valores de M² maiores que um, embora feixes de qualidade elevada possam ter valores muito próximos a um.

A abertura numérica de um feixe gaussiano é definida como sendo${\displaystyle \mathrm {NA} =n\sin \theta }$, onde n é o índice de refração do meio através do qual o feixe se propaga. Isto significa que o intervalo de Rayleigh está relacionado à abertuda numérica por

${\displaystyle z_{\mathrm {R} }=w_{0}/\mathrm {NA} }$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Potência e intensidade

Potência através de uma abertura

A potência P passando através de um círculo de raio r no plano transversal na posição z é^[9]

${\displaystyle P(r,z)=P_{0}\left[1-e^{-2r^{2}/w^{2}(z)}\right]\ ,}$

onde

${\displaystyle P_{0}={1 \over 2}\pi I_{0}w_{0}^{2}}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

é a potência total transmitida pelo feixe.

Para um círculo de raio ${\displaystyle r=w(z)\,}$, a fração de potência transmitida através do círculo é

${\displaystyle {P(z) \over P_{0}}=1-e^{-2}\approx 0.865\ .}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Similarmente, cerca de 90 porcento da potência do feixe irá fluir através de um círculo de raio ${\displaystyle r=1.07\cdot w(z)}$, 95 porcento através de um círculo de raio ${\displaystyle r=1.224\cdot w(z)}$, e 99 porcento através de um círculo de raio ${\displaystyle r=1.52\cdot w(z)}$.^[9] ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Intensidade de pico

A intensidade de pico em uma distância axial ${\displaystyle z}$ da largura do feixe pode ser calculada como o limite da potência delimitada com um círculo de raio ${\displaystyle r}$, dividida pela área do círculo ${\displaystyle \pi r^{2}}$ quando este encolhe (${\displaystyle r}$ tende a zero):

${\displaystyle I(0,z)=\lim _{r\to 0}{\frac {P_{0}\left[1-e^{-2r^{2}/w^{2}(z)}\right]}{\pi r^{2}}}}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

O limite pode ser avaliado utilizando a regra de L'Hôpital:

${\displaystyle I(0,z)=={\frac {P_{0}}{\pi }}\lim _{r\to 0}{\frac {\left[-(-2)(2r)e^{-2r^{2}/w^{2}(z)}\right]}{w^{2}(z)(2r)}}={2P_{0} \over \pi w^{2}(z)}.}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Parâmetros complexos do feixe

Ver artigo principal: Parâmetro complexo do feixe

O tamanho da cintura e a curvatura de um feixe gaussiano em função de z ao longo do feixe pode ser também codificada em parâmetro complexo do feixe ${\displaystyle q(z)}$^[10][11] dado por:

${\displaystyle q(z)=z+iz_{\mathrm {R} }\ .}$

Introduzindo esta complicação conduz a uma simplificação da equação de campo de feixe gaussiano como mostrado abaixo. Pode ser visto que o inverso de q(z) contém a curvatura da frente de onda e intensidade relativa no eixo em suas partes real e imaginária, respectivamente:^[10]

${\displaystyle {1 \over q(z)}={1 \over z+iz_{\mathrm {R} }}={z \over z^{2}+z_{\mathrm {R} }^{2}}-i{z_{\mathrm {R} } \over z^{2}+z_{\mathrm {R} }^{2}}={1 \over R(z)}-i{\lambda \over \pi w^{2}(z)}.}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

O parâmetro complexo do feixe simplifica a análise matemática da propagação do feixe gaussiano, e especialmente na análise de cavidades de ressonância óptica usando matrizes de transferência de raios.

Em seguida, utilizando esta fórmula, a equação anterior para o campo elétrico (ou magnético) é bastante simplificada. Se nós chamarmos u a força de campo relativa de um feixe gaussiano elíptico (com os eixos elípticos nas direções x e y) então ele pode ser separado em x e y de acordo com:

${\displaystyle {u}(x,y,z)={u_{x}}(x,z)\,{u_{y}}(y,z),}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde

${\displaystyle {u_{x}}(x,z)={\frac {1}{\sqrt {{q}_{x}(z)}}}\exp \left(-ik{\frac {x^{2}}{2{q}_{x}(z)}}\right)}$,

${\displaystyle {u_{y}}(y,z)={\frac {1}{\sqrt {{q}_{y}(z)}}}\exp \left(-ik{\frac {y^{2}}{2{q}_{y}(z)}}\right)}$,

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde ${\displaystyle q_{x}(z)}$ e ${\displaystyle q_{y}(z)}$ são os parâmetros complexos do feixe nas direções x e y.

Para o caso comum de um perfil de feixe circular, ${\displaystyle {q}_{x}={q}_{y}={q}}$ e ${\displaystyle x^{2}+y^{2}=r^{2}}$, que produz^[12]

${\displaystyle {u}(r,z)={\frac {1}{{q}(z)}}\exp \left(-ik{\frac {r^{2}}{2{q}(z)}}\right).}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Equação da onda

Como um caso especial de radiação eletromagnética, feixes de Gauss (e modos gaussianos de ordem superior detalhados abaixo) são soluções da equação da onda para um campo eletromagnético no espaço livre ou em um meio dielétrico homogêneo:^[13] obtidos pela combinação de equações de Maxwell para a ondulação de E e a ondulação de H, resultando em:

${\displaystyle \nabla ^{2}U={\frac {1}{c^{2}}}{\frac {\partial ^{2}U}{\partial t^{2}}},}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde c é a velocidade da luz no meio, e ${\displaystyle U}$ pode se referir ao vetor do campo elétrico ou campo magnético, à medida que qualquer solução específica para um determina o outro. A solução do feixe gaussiano é válida apenas para aproximações paraxiais, isto é, onde a propagação da onda é limitada a direções com um pequeno ângulo de um eixo. Sem perda de generalidade, vamos assumir que a direção a ser a direção +z em cujo caso a solução U pode geralmente ser escrita em termos de u que não tem dependência do tempo e varia de forma relativamente suave no espaço, com a maior variação correspondendo espacialmente ao número de onda k na direção z:^[13]

${\displaystyle U(x,y,z,t)=u(x,y,z)e^{-i(kz-\omega t)}\,{\hat {x}}\;.}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Usando esta fórmula juntamente com a aproximação paraxial, ${\displaystyle \partial ^{2}u/\partial z^{2}}$ pode ser então essencialmente negligenciada. Uma vez que soluções da equação da onda eletromagnética mantém apenas para para polarizações que são ortogonais à direção de propagação (z), consideramos sem perda de generalidade a polarização na direção x de modo que agora resolvemos a equação escalar para u(x,y,z).

Substituindo esta solução na equação da onda acima produz a aproximação paraxial para a equação escalar da onda:^[13]

${\displaystyle {\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}=2ik{\frac {\partial u}{\partial z}}.}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Solução no modo gaussiano

Pode ser verificado que o feixe gaussiano de qualquer cintura de feixe w₀ satisfaz esta equação da onda; isto é mais facilmente realizado expressando a onda em z em termos do parâmetro complexo do feixe q(z) como definido acima.

A segunda diferenciação da expressão de u(r,z) (onde r² = x² + y²) em relação a x produz:

${\displaystyle {\frac {\partial ^{2}u}{\partial x^{2}}}\;=\;u\left(-{\frac {ik}{q}}+\left({\frac {-ikx}{q}}\right)^{2}\right)\;=\;u\left(-{\frac {ik}{q}}-{\frac {k^{2}x^{2}}{q^{2}}}\right)}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

e da mesma forma para y. Formando a soma no lado esquerdo da equação escalar da onda acima, produz:

${\displaystyle {\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}\;=\;u\left(-2{\frac {ik}{q}}-{\frac {k^{2}r^{2}}{q^{2}}}\right)}$

Agora diferenciando u em relação a z, encontramos:

${\displaystyle {\frac {\partial ^{2}u}{\partial z^{2}}}\;=\;u\left(-{\frac {1}{q}}+{\frac {-ikr^{2}}{2q^{2}}}\right)\;}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

a partir do qual o lado direito da equação da onda é:

${\displaystyle 2ik{\frac {\partial ^{2}u}{\partial z^{2}}}\;=\;u\left(-{\frac {2ik}{q}}-{\frac {k^{2}r^{2}}{q^{2}}}\right)\;}$ ,

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

idêntico ao resultado acima para o lado esquerdo.

Outras soluções

Como esperado, encontramos que o feixe gaussiano é a solução para a equação da onda paraxial, entretanto existem muitas outras soluções. Como soluções para um sistema linear, qualquer combinação de soluções (utilizando adição ou multiplicação por uma constante) é também uma solução. A gaussiana fundamental passa a ser a que minimiza o produto do mínimo tamanho de cintura e divergência de campo distante, como notado acima. Em busca de soluções paraxiais, e sobretudo as que descrevem radiação laser que não estão no modo gaussiano fundamental, procuraremos famílias de soluções que gradualmente aumentam produtos de suas divergências e mínimos tamanhos de cintura. Duas importantes decomposições ortogonais deste tipo são os modos de Germite-Gauss ou Laguerre-Gauss, correspondendo, respectivamente, à simetria retangular e circular, como detalhado na próxima seção. Com ambos, o feixe gaussiano fundamental que temos considerado é o de ordem mais baixa.

Modos de ordem superior

Ver também: Transverse mode

Modos de Hermite-Gauss

Doze modos de Hermite-Gauss

É possível decompor um feixe paraxial coerente usando um conjunto ortogonal de chamados modos de Hermite-Gauss, qualquer um dos quais é dado pelo produto de um fator em x e um fator em y. Uma solução escrita em coordenas cartesianas é possível devido à separabilidade em x e y na equação paraxial de Helmholtz.^[14] Assim dado um modo de ordem (l,m) referindo às direções x e y, a amplitude do campo elétrico em x,y,z pode ser dado por: ${\displaystyle E(x,y,z)=u_{l}(x,z)u_{m}(y,z)}$ onde os fatores para dependência de x e y são dados cada um por:

${\displaystyle {u}_{J}(x,z)=\left({\frac {\sqrt {2/\pi }}{2^{J}\;J!\;w_{0}}}\right)^{\!\!1/2}\!\!\left({\frac {{q}_{0}}{{q}(z)}}\right)^{\!\!1/2}\!\!\left(-{\frac {{q}^{\ast }(z)}{{q}(z)}}\right)^{\!\!J/2}\!\!H_{J}\left({\frac {{\sqrt {2}}x}{w(z)}}\right)\,\exp \!\left(\!-i{\frac {kx^{2}}{2{q}(z)}}\right)}$ ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde utilizamos o parâmetro complexo do feixe q(z) (como definido acima) para um feixe de cintura w₀ em z a partir do foco. Desta forma, o primeiro fator é apenas uma constante normalizadora para formar o conjunto de u_J ortonormal. O segundo fator é uma normalização adicional dependente em z que compensa a expansão da extensão espacial do modo de acordo com w(z)/w₀ (devido aos dois últimos fatores). Ele também contém parte da fase de Gouy. O terceiro fator é uma fase pura que aumenta a mudanca de fase de Gouy para altas ordens J.

Os dois fatores finais representam a variação espacial sobre x (ou y). O quarto fator é o polinômio de Hermite de ordem ${\displaystyle J}$ ("forma de físicos", i.e. ${\displaystyle H_{1}(x)=2x\,}$), enquanto o quinto representa queda de amplitude gaussiana ${\displaystyle \exp(-x^{2}/w(z)^{2})}$, embora isto não seja óbvio utilizando o complexo q no expoente. Expansão da exponencial também produz um fator de fase em x que representa a curvatura de frente de onda (1/R(z)) em z ao longo do feixe.

Modos de Hermite-Gauss são tipicamente designados "TEM_lm"; o feixe gaussiano fundamental pode assim ser referido como TEM₀₀ (onde TEM significa Transverse electro-magnetic). Multiplicando u_l(x,z) e u_m(y,z) para obter o perfil em modo 2D, e removendo a normalização de modo que o perfil principal é simplesmente chamado E₀, podemos escrever o modo (l,m) na forma mais acessível: ${\displaystyle E_{l,m}(x,y,z)=E_{0}{\frac {w_{0}}{w(z)}}\!\ H_{l}\!\!\left({\frac {{\sqrt {2}}\,x}{w(z)}}\right)\!H_{m}\!\!\left({\frac {{\sqrt {2}}\,y}{w(z)}}\right)\,\exp \!\!\left(\!-{\frac {x^{2}+y^{2}}{w^{2}(z)}}\right)\times }$ ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

${\displaystyle \exp \!\left(\!-i{\frac {k(x^{2}+y^{2})}{2R(z)}}\right)\exp(\!-ikz)\exp(i\psi (z))\;\;}$ .

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Nesta fórmula, o parâmetro w₀, como anteriormente, determina a família de modos, em particular escalando a extensão espacial da cintura do modo fundamental e todos os outros padrões de modo em z=0. Dado w₀, w(z) e R(z) tem as mesmas definições como para o feixe gaussiano fundamental descrito acima. Pode ser visto que com l=m=0 obtemos o feixe gaussiano fundamental descrito anteriormente (desde que H₀ = 1). A única diferença específica nos perfis x e y em qualquer z são devido aos fatores de polinomiais de Hermite para os números de ordem l e m. Entretanto há uma mudanca na evolução da fase de Gouy dos modos sobre z:

${\displaystyle \psi (z)=(N+1)\,\arctan \left({\frac {z}{z_{\mathrm {R} }}}\right)}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde a ordem combinada do modo N é definido como N=l+m. Enquanto a mudança de fase de Gouy para o modo gaussiano fundamental (0,0) apenas varia por ±π/2 radianos sobre todo z (e apenas por ±π/4 radianos entre ±Z_R), este é aumentado por um fator N+1 para os modos de ordem superior.^[15]

Modos de Hermite-Gauss, com suas simetrias retangulares, são especialmente adequados para análise modal de radiação de radiação de lasers cujos projetos de cavidades são assimétricos em uma forma retangular. Por outro lado, lasers e sistemas com simetria circular podem ser melhor manipulados utilizando o conjunto de modos Lageurre-Gauss introduzidos na próxima seção.

 Modos de Laguerre-Gauss

Perfis de feixe que são circularmente simétricos (ou lasers com cavidades que são cilindricamente simétricas) são frequentemente resolvidos utilizando a decomposição modal de Laguerre-Gauss.^[16] Estas funções são escritas em coordenadas cilíndricas usando polinômios de Laguerre. Cada modo transversal é novamente rotulado utilizando dois inteiros, neste caso o índice radial ${\displaystyle p\geq 0}$ e o índice azimutal ${\displaystyle l}$ que pode ser positivo ou negativo (ou zero).

${\displaystyle {u}(r,\phi ,z)={\frac {C_{lp}^{LG}}{w(z)}}\left({\frac {r{\sqrt {2}}}{w(z)}}\right)^{\!|l|}\exp \!\left(\!-{\frac {r^{2}}{w^{2}(z)}}\right)L_{p}^{|l|}\!\left({\frac {2r^{2}}{w^{2}(z)}}\right)\times }$

${\displaystyle \exp \!\left(\!-ik{\frac {r^{2}}{2R(z)}}\right)\exp(il\phi )\,\exp(\!-ikz)\,\exp(i\psi (z))\;\;}$ .

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

^[17]

onde ${\displaystyle L_{p}^{l}}$ são os polinômios generalizados de Laguerre. ${\displaystyle C_{lp}^{LG}}$ é uma constante normalizada requerida nao detalhada aqui; ${\displaystyle w(z)}$ e ${\displaystyle R(z)}$ tem as mesmas definições como acima. Tal como os modos de Hermite-Gauss de ordem superior a magnitude da mudança de fase de Gouy dos modos de Laguerre-Gauss é exagerado pelo fator N+1:

${\displaystyle \psi (z)=(N+1)\,\arctan \left({\frac {z}{z_{\mathrm {R} }}}\right)}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde neste caso o número de modo combinado N = |l| + 2p. Como anteriormente, as variações de amplitude transversal são contidas nos dois últimos fatores da linha superior da equação, que novamente inclui a queda gaussiana básica em r mas agora multiplicado por um polinômio de Laguerre. O efeito do número do modo de rotação l, além de afetar o polinômio de Laguerre, está principalmente contido no fator de fase exp(-ilφ), em que o perfil do feixe é avançado (ou retardado) por l fases completas 2π em uma rotação em torno do feixe (in φ). Este é um exemplo de um vórtex óptico de carga topológica l, e pode ser associado com o momento angular orbital da luz neste modo.

 Modos de Ince-Gauss

Em coordenadas elípticas, pode se escrever os modos de ordem superior utilizando polinômios de Ince. Os modos de Ince-Gauss pares e ímpares são dados por ^[18]

${\displaystyle u_{\varepsilon }\left(\xi ,\eta ,z\right)={\frac {w_{0}}{w\left(z\right)}}\mathrm {C} _{p}^{m}\left(i\xi ,\varepsilon \right)\mathrm {C} _{p}^{m}\left(\eta ,\varepsilon \right)\exp \left[-ik{\frac {r^{2}}{2q\left(z\right)}}-\left(p+1\right)\zeta \left(z\right)\right],}$

onde ${\displaystyle \xi }$ e ${\displaystyle \eta }$ são as coordenadas elípticas radial e angular definidas por

${\displaystyle x={\sqrt {\varepsilon /2}}w\left(z\right)\cosh \xi \cos \eta ,}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

${\displaystyle y={\sqrt {\varepsilon /2}}w\left(z\right)\sinh \xi \sin \eta .}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

${\displaystyle {C}_{p}^{m}\left(\eta ,\varepsilon \right)}$ são os mesmos polinômios de Ince de ordem ${\displaystyle p}$ e grau ${\displaystyle m}$onde ${\displaystyle \varepsilon }$ é o parâmetro de elipticidade. Os modos de Hermite-Gauss e Laguerre-Gauss são um caso especial dos modos de Ince-Gauss para ${\displaystyle \varepsilon =\infty }$ e ${\displaystyle \varepsilon =0}$ respectivamente.

 Modos Hipergeométrico-Gauss

Há uma outra importante classe de modos de onda paraxial em coordenadas polares em que a amplitude complexa é proporcional a uma função hipergeométrica confluente.

Estes modos tem um perfil de fase singular e são funções próprias do momento angular orbital do fóton. O perfil de intensidade é caracterizado por um anel brilhante único com uma singularidade em seu centro, onde a amplitude do campo desaparece. A amplitude é escrita em termos da coordenada radial adimensional ${\displaystyle \rho =r/w_{0}}$ e a coordenada longitudinal adimensional ${\displaystyle \mathrm {Z} =z/z_{R}}$.^[19]

${\displaystyle u_{pm}(\rho ,\theta ;\mathrm {Z} )={\sqrt {\frac {2^{p+|m|+1}}{\pi \Gamma (p+|m|+1)}}}{\frac {\Gamma (1+|m|+{\frac {p}{2}})}{\Gamma (|m|+1)}}\,\,i^{|m|+1}\mathrm {Z} ^{\frac {p}{2}}(\mathrm {Z} +i)^{-(1+|m|+{\frac {p}{2}})}\rho ^{|m|}e^{-{\frac {i\rho ^{2}}{(\mathrm {Z} +i)}}}e^{im\phi }{}_{1}F_{1}\left(-{\frac {p}{2}},|m|+1;{\frac {r^{2}}{\mathrm {Z} (\mathrm {Z} +i)}}\right),}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde ${\displaystyle m}$ é inteiro, ${\displaystyle p\geq -|m|}$ é real com valor, ${\displaystyle \Gamma (x)}$ é a função gama e ${\displaystyle {}_{1}F_{1}(a,b;x)}$ é a função hipergeométrica confluente.

Algumas subfamílias de modos hipergeométrico-Gauss (HyGG) podem ser listados como modos de Bessel-Gauss modificados, os modos gaussianos exponenciais modificados, e os modos de Laguerre–Gauss.

O conjunto de modos hipergeométrico-Gauss é supercompleto e não é um conjunto ortogonal de modos. Apesar de seu perfil de campo complicado, modos HyGG tem um perfil muito simples no plano da pupila (${\displaystyle \mathrm {Z} =0}$):

${\displaystyle u(\rho ,\phi ,0)\propto \rho ^{p+|m|}e^{-\rho ^{2}+im\phi }.}$

Veja vórtex óptico, que explica que a onda de saída de um holograma pitch-fork é uma subfamília dos modos HyGG. O perfil HyGG enquanto o feixe propaga ao longo de ${\displaystyle \zeta }$ tem uma mudança dramática e não é um modo estável abaixo do intervalo de Rayleigh.

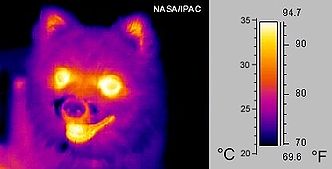
A Irradiação ou radiação térmica é a radiação eletromagnética gerada pelo movimento térmico das partículas carregadas na matéria. Toda matéria com uma temperatura maior que o zero absoluto emite radiação térmica. O movimento de partículas resulta em aceleração de carga ou oscilação de dipolo que produz radiação eletromagnética; no entanto, uma interferência destrutiva pode cancelar toda a radiação. Muitas vezes a irradiação térmica é chamada de radiação de corpo negro, uma radiação eletromagnética térmica dentro ou ao redor de um corpo, se um objeto emissor de radiação atende às características físicas de um corpo negro em equilíbrio termodinâmico. Exemplos de radiação térmica incluem a luz visível e a luz infravermelha emitidas por uma lâmpada incandescente, a radiação infravermelha emitida por animais e detectada por câmeras de infravermelho, e micro-ondas cósmicas.

Índice

• 1Mecanismo de geração e características da Radiação Térmica
  • 1.1Propriedades
  • 1.2Cor observada pelo olho humano emitida por um corpo negro
• 2Calor: Radiação Térmica entre dois corpos
  • 2.1Classificação da matéria quanto à propagação de calor
• 3Corpo Negro e Radiação Térmica
• 4Leis de Wien e de Planck
• 5Lei de Stefan-Boltzmann
• 6Ver também
• 7Referências

Mecanismo de geração e características da Radiação Térmica

Imagem de um pequeno cão visto em infravermelho.

A radiação térmica é gerada pelo movimento de partículas carregadas na matéria. Toda substância com temperatura maior do que 0 K (zero Kelvin; Zero absoluto) emite radiação térmica.^[1] Átomos e moléculas que compõem a matéria possuem energia cinética que varia, e essas mudanças de energia acabam resultando em aceleração das partículas e oscilações das cargas que compõem os átomos. Essa movimentação das cargas na matéria gera a radiação eletromagnética, ou seja, a energia cinética de átomos e moléculas converte-se em energia térmica e resulta na radiação eletromagnética térmica.

As características da radiação térmica dependem de várias propriedades da superfície irradiante, incluindo temperatura, capacidade de absorção espectral e poder de emissividade espectral, como concluiu Kirchhoff em seus estudos.^[1] A radiação não é monocromática, ou seja, não consiste em uma única frequência de comprimento de onda, mas sim na dispersão contínua de energia das partículas. Absorção, refletividade e emissividade dependem do comprimento de onda da radiação, e a temperatura determina a distribuição dos comprimentos de onda emitidos.

Propriedades

Há quatro propriedades gerais que caracterizam a irradiação térmica:^[2]

• a radiação térmica emitida por um corpo negro em qualquer temperatura possui vários comprimentos de onda e frequências. A distribuição da frequência é dada pela Lei de Planck para um emissor ideal;

• o intervalo dominante de frequências aumenta proporcionalmente com a temperatura, conforme a Lei de Wien;

• a quantidade total de radiação, em todas frequências, aumenta de acordo com a temperatura elevada à sua quarta potência, conforme a Lei de Stefan-Boltzmann;

• a taxa de radiação eletromagnética emitida em determinada frequência é proporcional ao total absorvido pelo corpo à mesma frequência. Assim, uma superfície que absorve mais a luz vermelha irradia termicamente mais a luz vermelha. Este princípio é aplicado a todas as demais propriedades de onda, inclusive comprimento de onda (cor), direção, polarização e coerência. Portanto, é possível ter irradiação térmica direcional, polarizada e coerente, embora isso, na natureza, seja muito raro longe de sua fonte.

Cor observada pelo olho humano emitida por um corpo negro

O metal aquecido a temperatura próxima à de fusão emite radiação no infravermelho e no visível próximo ao infravermelho. O primeiro é invisível ao olho humano, mas o segundo pode ser percebido pelo brilho avermelhado.

°C (K)	Cor[3]
480 °C (753,15 K)	brilho avermelhado fraco
580 °C (853,15 K)	vermelho escuro
730 °C (1 003,15 K)	vermelho brilhante, levemente alaranjado
930 °C (1 203,15 K)	laranja brilhante
1 100 °C (1 373,15 K)	laranja amarelado pálido
1 300 °C (1 573,15 K)	amarelo claro
> 1 400 °C (1 673,15 K)	branco (amarelado se visto a distâncias superiores à da atmosfera)

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Calor: Radiação Térmica entre dois corpos

Ver artigo principal: Calor

Como qualquer corpo com temperatura diferente de 0 K emite radiação térmica, um segundo corpo pode absorver essas ondas na forma de energia eletromagnética que se propagam pelo espaço, tendendo a entrar em equilíbrio termodinâmico com o primeiro. Esse evento é chamado de transferência de energia térmica, isto é, calor. A emissão de radiação não cessa após o equilíbrio térmico, pois todo corpo que tenha agitação térmica, ou seja, temperatura, mesmo que próxima a 0 K, irradia sua energia.

Como as ondas eletromagnéticas também podem se propagar no vácuo, a transferência de calor de um corpo a outro ocorre mesmo se não existir meio material entre os dois, como é o caso da energia emitida pelo Sol e que chega à Terra. O mesmo não ocorre com condução térmica nem com convecção.

Classificação da matéria quanto à propagação de calor

Nem todos meios materiais permitem a propagação das ondas de calor através deles. Assim, pode-se classificá-los em:

• Diatérmicos: meios que permitem a propagação das ondas de calor através deles (são transparentes às ondas de calor). Exemplo: ar;

• Atérmicos: meios que não permitem a propagação das ondas de calor através deles (são opacos às ondas de calor). Exemplo: parede de tijolos.

Corpo Negro e Radiação Térmica

Ver artigo principal: Corpo negro

Corpo negro é aquele que absorve toda a radiação eletromagnética que nele incide, ou seja, nenhuma onda o atravessa (somente em casos específicos) nem é refletida. Tal corpo, a princípio, não pode ser visto,^[4] advindo desse o nome corpo negro. Apesar disso, corpos negros emitem radiação, o que permite determinar sua temperatura. Em equilíbrio termodinâmico (em temperatura constante), um corpo negro ideal irradia energia na mesma taxa que a absorve,^[4] sendo essa uma das propriedades que o tornam uma fonte ideal de radiação térmica^[5] (chamada de radiação de corpo negro).^[6] Corpos negros não existem na natureza, visto que nenhum objeto tem absorção e emissão perfeitas. A emissividade de um corpo é definida pela relação entre sua radiância e a do corpo negro.

Leis de Wien e de Planck

Ver artigo principal: Lei de Wien

Ver artigo principal: Lei de Planck

Leis de Wien e de Planck: à medida que a temperatura diminui, o pico da curva da radiação de um corpo negro se desloca para menores intensidades e maiores comprimentos de onda.

A figura ao lado mostra o espectro da radiação térmica emitida por corpos a várias temperaturas. Ao incidir sobre um corpo, parte da radiação térmica é absorvida (a), parte é refletida (r), e o resto é transmitido (t). A partir do princípio de conservação de energia, tem-se que:

${\displaystyle a+r+t=1}$^[7]

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

A Lei de Wien relaciona o comprimento de onda em que há máxima emissão de radiação de corpo negro com uma temperatura e determina que o comprimento de onda emitido diminui com o aumento da temperatura:

${\displaystyle \lambda _{max}={\frac {b}{T}}}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde:

${\displaystyle \lambda _{max}\,}$ é o comprimento de onda (em metros) no qual a intensidade da radiação eletromagnética é a máxima;

${\displaystyle T\,}$ é a temperatura do corpo negro em Kelvin (K), e

${\displaystyle b\,}$ é a constante de proporcionalidade, chamada constante de dispersão de Wien, em Kelvin-metros (K • m).

A Lei de Planck para radiação de corpo negro exprime a radiância espectral em função do comprimento de onda e da temperatura do corpo negro e fornece a distribuição dos comprimentos de onda no espectro em função da temperatura. A maior parte da irradiação ocorre em um comprimento de onda específico, chamado de comprimento de onda principal de irradiação, que depende da temperatura do corpo. Quanto maior a temperatura, maior a frequência da radiação e menor é o comprimento de onda:

${\displaystyle I(\nu ,T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{e^{\frac {h\nu }{kT}}-1}}}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde:

${\displaystyle I\,}$ é a radiância espectral medida em J•s⁻¹•m⁻²•sr⁻¹•Hz⁻¹

${\displaystyle \nu \,}$ é a frequência medida em Hertz (Hz)

${\displaystyle T\,}$ é a temperatura do corpo negro medida em Kelvin (K)

${\displaystyle h\,}$ é a constante de Planck medida em Joule por Hertz (J/Hz)

${\displaystyle c\,}$ é a constante velocidade da luz medida em metros por segundo (m/s)

${\displaystyle e\,}$ é o número de Euler

${\displaystyle k\,}$ é a constante de Boltzmann medida em Joule por Kelvin (J/K)

Relacionando com o espectro visível, devido ao comprimento de onda, objetos com temperaturas altas produzem luz de coloração próxima ao azul, enquanto objetos com temperaturas não tão altas podem gerar luz avermelhada (a faixa do espectro seguinte à visível é justamente o infravermelho). Por exemplo, um objeto vermelho quente irradia principalmente ondas longas da faixa visível do espectro (luzes avermelhada e alaranjada). Se for aquecido, passará a emitir menores comprimentos de onda (luzes azulada e esverdeada), e a distribuição das frequências faz a luz parecer branca aos olhos humanos. Esse efeito é chamado de "branco quente". Entretanto, mesmo em temperaturas superiores a 2 000 K, 99% da energia irradiada está na faixa do infravermelho do espectro. Em outros casos, a matéria pode irradiar comprimentos de onda que não podem ser vistos pelo olho humano, como quando a temperatura é relativamente baixa ou extremamente alta.

Lei de Stefan-Boltzmann

Ver artigo principal: Lei de Stefan-Boltzmann

Lei de Stefan-Boltzmann: a energia total emitida por um corpo é diretamente proporcional à quarta potência de sua temperatura. Em azul, o gráfico da energia total emitida calculado por Wien.

A Lei de Stefan-Boltzmann estabelece que a energia total irradiada por unidade de área superficial de um corpo negro, na unidade de tempo (radiação do corpo negro), ou densidade de fluxo energético, indicada por j*, é diretamente proporcional à quarta potência da sua temperatura absoluta:

${\displaystyle j^{\star }=\sigma T^{4}}$^[8]

${\displaystyle \sigma =5,6697\times 10^{-8}Wm^{-2}K^{-4}}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde:

${\displaystyle j^{\star }}$ é a energia total irradiada por um corpo negro por unidade de área, medida em Watts por metro quadrado (W / m²)

${\displaystyle T}$ é a temperatura do corpo em Kelvin (K)

${\displaystyle \sigma }$ é a constante de Stefan-Boltzmann

Na radiometria, a irradiância é o fluxo radiante^[1] recebido por uma superfície pela unidade de área.

Definições matemáticas

A irradiância de uma superfície, denotada E_e ("E" para "energética", para evitar a confusão com quantidades fotométricas), é definida como

${\displaystyle E_{\mathrm {e} }={\frac {\partial \Phi _{\mathrm {e} }}{\partial A}},}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde

• ∂ é o símbolo derivada parcial;
• Φ_e é o fluxo radiante recebido;
• A é a área.

Se quisermos falar sobre o fluxo radiante "emitido" por uma superfície, falamos de emitância radiante.^[1]

A lei de Beer-Lambert, também conhecida como lei de Beer ou lei de Beer-Lambert-Bouguer é uma relação empírica que, na Óptica, relaciona a absorção de luz com as propriedades do material atravessado por esta.

Índice

• 1Equações
• 2Lei de Beer-Lambert na atmosfera
• 3Referências
• 4História
• 5Ligações externas
• 6Ver também

Equações

Isto se pode expressar de distintas maneiras:

${\displaystyle {\begin{matrix}A=\alpha lc\end{matrix}}}$

${\displaystyle {I_{1} \over I_{0}}=10^{-\alpha lc}}$

${\displaystyle A=-\log {\frac {I_{1}}{I_{0}}}}$

${\displaystyle \alpha ={\frac {4\pi k}{\lambda }}}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Onde:

• A é a absorbância (ou absorvância)
• I₀ é a intensidade da luz incidente
• I₁ é a intensidade da luz uma vez tendo atravessado o meio
• l é a distância que a luz atravessa pelo corpo
• c é a concentração de substância absorvente no meio
• α é a absorbtividade molar da substância
• λ é o comprimento de onda do feixe de luz
• k é o coeficiente de extinção

Em resumo, a lei explica que há uma relação exponencial entre a transmissão de luz através de uma substância e a concentração da substância, assim como também entre a transmissão e a longitude do corpo que a luz atravessa. Se conhecemos l e α, a concentração da substância pode ser deduzida a partir da quantidade de luz transmitida.

As unidades de c e α dependem do modo em que se expressa a concentração da substância absorvente. Se a substância é líquida, se deve expressar como uma fração molar. As unidades de α são o inverso do comprimento (por exemplo cm⁻¹). No caso dos gases, c pode ser expressada como densidade (a longitude ao cubo, por exemplo cm⁻³), em cujo caso α é uma seção representativa da absorção e tem as unidades em comprimento ao quadrado (cm², por exemplo). Se a concentração de c está expressa em moles por volume, α é a absorvância molar normalmente dada em mol cm⁻². No entanto, também pode-se tratar de uma suspensão e aí a unidade de concentração é expressa em FTU.

O valor do coeficiente de absorção α varia segundo os materiais absorventes e com o comprimento de onda para cada material em particular. Deve ser determinado experimentalmente.

A lei tende a não ser válida para concentrações muito elevadas, especialmente se o material dispersa muito a luz.

A relação da lei entre concentração e absorção de luz é a base do uso de espectroscopia para determinar a concentração de substâncias em química analítica.

Lei de Beer-Lambert na atmosfera

Esta lei também se aplica para descrever a atenuação da radiação solar ao passar através da atmosfera. Neste caso há dispersão da radiação além da absorção. A lei de Beer-Lambert para a atmosfera é expressa por:

${\displaystyle I_{n}=I_{0}\,\exp(-(k_{a}+k_{g}+k_{NO_{2}}+k_{w}+k_{O_{3}}+k_{r})m)}$ ,

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde cada ${\displaystyle k_{x}}$ é um coeficiente de extinção cujo sub-índice identifica a fonte de absorção ou dispersão:

• ${\displaystyle a}$ faz referência a aerossóis densos (que absorvem e dispersam)
• ${\displaystyle g}$ são gases uniformemente misturados (principalmente dióxido de carbono (${\displaystyle CO_{2}}$) e oxigênio molecular (${\displaystyle O_{2}}$) que só absorvem)
• ${\displaystyle NO_{2}}$ é dióxido de nitrogênio, devido principalmente à contaminação (só absorve)
• ${\displaystyle w}$ é a absorção produzida pelo vapor de água
• ${\displaystyle O_{3}}$ é ozônio (só absorção)
• ${\displaystyle r}$ é a dispersão de Rayleigh para o oxigênio molecular (${\displaystyle O_{2}}$) e nitrogênio (${\displaystyle N_{2}}$) (responsável pela cor azul do céu).

Os potenciais de Liènard-Wiechert são a descrição matemática clássica dos potenciais escalar e vetorial de uma carga pontual em movimento. Sua derivação se origina das equações de Maxwell e portanto não é válida no domínio da mecânica quântica.

Potenciais retardados

Pode-se fazer cálculo para determinar os potenciais gerados por uma distribuição qualquer de cargas no espaço, dependentes do tempo. Nesta demonstração, chegamos a conclusão de que os potenciais gerador por uma distribuição dependente do tempo, em um ponto r, num instante de tempo t dependem desta distribuição num instante anterior que é denominado na literatura de tempo retardado. Escrevemos para o potencial elétrico:

${\displaystyle \varphi (\mathbf {r} ,t)=\int {\frac {1}{4\pi \epsilon _{0}}}{\frac {\rho (\mathbf {r} ',t_{r})}{|\mathbf {r} -\mathbf {r} '|}}d^{3}r'}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Aqui, ${\displaystyle \rho }$ é a densidade de cargas avaliada no tempo retardado ${\displaystyle t_{r}}$ e ${\displaystyle \mathbf {r'} }$ é posição das cargas. O tempo retardado é definido como:

${\displaystyle t=t_{r}+{\frac {|\mathbf {r} -\mathbf {r} '|}{c}}}$

Ou seja, o tempo retardado é devido a um tempo de propagação finito com velocidade c (velocidade da luz), e ${\displaystyle |\mathbf {r} -\mathbf {r} '|/c}$ é o tempo que o sinal levou para se propagar até o ponto ${\displaystyle \mathbf {r} }$. Note que ${\displaystyle \mathbf {r'} }$ deve ser avaliado no tempo retardo também. Analogamente, podemos escrever para o potencial vetor magnético:

${\displaystyle \mathbf {A} (\mathbf {r} ,t)=\int {\frac {\mu _{0}}{4\pi }}{\frac {\mathbf {J} (\mathbf {r} ',t_{r})}{|\mathbf {r} -\mathbf {r} '|}}d^{3}r'}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Onde ${\displaystyle \mathbf {J} }$ é densidade volumétrica de corrente. É possível particularizar para os casos em 1 e 2 dimensões. Estes são os chamados potenciais retardados de uma distribuição de cargas e correntes.

Demonstração dos potenciais de Liènard-Wiechert

Estamos em condições de deduzir os potenciais de Liènard-Wiechert para uma carga pontual q em movimento, partindo dos potenciais retardados. O problema se torna muito simples com o uso da função delta de Dirac (${\displaystyle \delta (x)}$), que tem a seguinte propriedade:

${\displaystyle \int _{-\infty }^{\infty }\delta (x)dx=1}$

${\displaystyle \int _{-\infty }^{\infty }f(x)\delta (x-x_{0})dx=f(x_{0})}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Primeiramente, vamos utilizar estas ideias para escrever a densidade de cargas no instante ${\displaystyle t_{r}}$.

${\displaystyle \rho (\mathbf {r'} ,t_{r})=\int dt'\rho (\mathbf {r'} ,t')\delta (t'-t_{r})}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Sendo a carga na posição ${\displaystyle \mathbf {w} }$ no tempo ${\displaystyle t_{r}}$, escrevemos a densidade de cargas na forma:

${\displaystyle \rho (\mathbf {r'} ,t')=q\delta (\mathbf {r'-w} )}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Inserindo estas definições na integral para o potencial elétrico, obtemos:

${\displaystyle \varphi (\mathbf {r} ,t)=\int \int {\frac {1}{4\pi \epsilon _{0}}}{\frac {q\delta (\mathbf {r'-w} )\delta (t'-t_{r})}{|\mathbf {r} -\mathbf {r} '|}}d^{3}r'dt'}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

As funções Delta nos permite eliminar as integrais e após alguns passos não triviais, obtemos:

${\displaystyle \varphi (\mathbf {r} ,t)={\frac {1}{4\pi \epsilon _{0}}}{\frac {qc}{c|\mathbf {r} -\mathbf {w} |-(\mathbf {r} -\mathbf {w} )\cdot \mathbf {v} }}}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Onde ${\displaystyle \mathbf {v} }$ é a velocidade da partícula e definida como ${\displaystyle \mathbf {v} :={\frac {d\mathbf {w} }{dt}}}$. Obtemos assim o potencial elétrico para uma carga pontual. Este é um dos potenciais de Liènard-Wiechert. O potencial vetor pode ser deduzido de maneira análoga, notando que este pode ser escrito na forma:

${\displaystyle \mathbf {A} (\mathbf {r} ,t)=\int {\frac {\mu _{0}}{4\pi }}{\frac {\mathbf {v} \rho (\mathbf {r} ',t_{r})}{|\mathbf {r} -\mathbf {r} '|}}d^{3}r'}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Adotando os mesmos passos, obtemos:

${\displaystyle \mathbf {A(r} ,t)={\frac {\mu _{0}}{4\pi }}{\frac {qc\mathbf {v} }{c|\mathbf {r-w} |-(\mathbf {r-w} )\cdot \mathbf {v} }}}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

A dedução dos potenciais está completa. Podemos fazer uma relação bem simples entre os dois:

${\displaystyle \mathbf {A(r} ,t)={\frac {\mathbf {v} }{c^{2}}}\varphi (\mathbf {r} ,t)}$

 ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Lembrando que ${\displaystyle \mathbf {v} }$ e ${\displaystyle \mathbf {w} }$ devem ser avaliados no tempo retardado. Escrito desta forma, fica evidente que o potencial vetor tem a mesma direção da velocidade da partícula.

Referências