TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Espectro da radiação de corpo negro para diversas temperaturas.

A radiação do corpo negro é a radiação eletromagnética térmica dentro ou ao redor de um corpo em equilíbrio termodinâmico com seu ambiente, ou emitida por um corpo negro, um corpo hipotético opaco e não reflexivo que absorve toda a radiação eletromagnética que nele incide e emite radiação eletromagnética térmica, que é o resultado do movimento acelerado de partículas carregadas.^[1]

Em um material aquecido, a temperatura está associada à energia cinética dos átomos. Um aumento de temperatura implica em mais energia cinética fornecida para os átomos que constituem o material. Estes emitem luz a partir de partículas carregadas^[2] em movimento, gerando radiação eletromagnética.

A radiação do corpo negro tem um espectro específico e intensidade que depende apenas da temperatura do corpo, o que é assumido por uma questão de cálculos e teoria para ser uniforme e constante. Todos os corpos emitem radiação térmica, mas não necessariamente na faixa do visível, e à medida que se aumenta a temperatura a radiação é alterada.

Os cientistas do século XIX tentaram explicar as leis da radiação do corpo negro construindo um modelo da radiação eletromagnética em termos de ondas e usando a física clássica para derivar suas características. Eles, entretanto, descobriram, com muita surpresa, que as características deduzidas não estavam de acordo com as observações experimentais. De acordo com a física clássica, qualquer objeto muito quente deveria devastar a região em volta dele com suas radiações de alta frequência. Até mesmo o corpo humano, em 37oC, deveria brilhar no escuro. Não existiria, de fato, a escuridão.^[3]

Índice

• 1Lei de Stefan-Boltzmann
• 2Ver também
• 3Referências
• 4Bibliografia

Lei de Stefan-Boltzmann

Ver artigo principal: Lei de Stefan-Boltzmann

Em 1879, o físico Josef Stefan analisou o aumento do brilho de um corpo negro quando era aquecidos e descobriu que a intensidade total emitida em todos os comprimentos de onda era proporcional a quarta potência da temperatura. Esse resultado deu origem a Lei de Stefan-Boltzmann, usualmente descrita como:

${\displaystyle {\frac {_{\mbox{potência emitida}}}{_{\mbox{área superficial}}}}=constante\times T^{4}}$

Em que ${\displaystyle T}$ é a temperatura absoluta em escala Kelvin. A potência emitida é dada em Watt e a área superficial é dada em metros quadrados. O valor experimental da constante é ${\displaystyle 5,67\times 10^{-8}Wm^{-2}K^{-4}}$.^[4]

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

O metal aquecido a temperatura próxima à de fusão emite radiação no infravermelho e no visível próximo ao infravermelho. O primeiro é invisível ao olho humano, mas o segundo pode ser percebido pelo brilho avermelhado.

O ponto de Draper é a temperatura aproximada acima da qual quase todos os materiais sólidos brilham visivelmente como resultado da radiação de corpo negro.^[1][2][3] Foi estabelecido em 525° C (798 K) por John William Draper em 1847.^[4]

Corpos a temperaturas logo abaixo do ponto Draper irradiam principalmente na faixa infravermelha e emitem luz visível insignificante. O valor do ponto de Draper pode ser calculado usando a lei de deslocamento de Wien: a freqüência ${\displaystyle \nu _{\text{pico}}}$ (em hertz) emitida por um corpo negro se relaciona com a temperatura da seguinte forma^[5]

${\displaystyle \nu _{\text{pico}}=2.821{\frac {kT}{h}},}$

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde

k é Constante de Boltzmann,

h é Constante de Planck,

T é temperatura (em kelvins).

Substituir o ponto de Draper nesta equação produz uma freqüência de 83 THz, ou um comprimento de onda de 3,6 µm, que é bem dentro do infravermelho e completamente invisível ao olho humano. No entanto, a borda principal da curva de radiação do corpo negro se estende, em uma pequena fração do pico da intensidade, para o infravermelho próximo e vermelho-escuro (aproximadamente o intervalo 0,7-1 m), que são muito fracamente visíveis como um vermelho opaco.

De acordo com a lei de Stefan-Boltzmann, um corpo negro no ponto Draper emite 23 quilowatts de radiação por metro quadrado, quase exclusivamente infravermelho.

Cor observada pelo olho humano emitida por um corpo negro

°C (K)	Cor[6]
480 °C (753,15 K)	brilho avermelhado fraco
580 °C (853,15 K)	vermelho escuro
730 °C (1003,15 K)	vermelho brilhante, levemente alaranjado
930 °C (1203,15 K)	laranja brilhante
1100 °C (1373,15 K)	laranja amarelado pálido
1300 °C (1573,15 K)	amarelo claro
> 1400 °C (1673,15 K)	branco (amarelado se visto a distâncias superiores à da atmosfera)

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Espectro Visível convencional

Característica	Extremo vermelho	Extremo violeta
Frequência	400 THz	750 THz
Comprimento de onda:	750 nm	400 nm

Espectro eletromagnético completo (clique para ampliar)

Espectro visível (ou espectro óptico) é a porção do espectro eletromagnético cuja radiação é composta por fótons capazes de sensibilizar o olho humano de uma pessoa normal. Identifica-se a correspondente faixa de radiação por luz visível, ou simplesmente luz.

A faixa visível do espectro eletromagnético é delimitada junto à mais baixa frequência oticamente estimulante - percebida como vermelha - pela sugestivamente nomeada faixa de radiação infravermelha, e pelo lado da mais alta frequência perceptível - entendida como violeta - pela nomeada de forma igualmente sugestiva faixa de radiação ultravioleta.

Para cada comprimento de onda pertencente à faixa de luz visível encontra-se associada a percepção de uma cor.

Espectro da luz visível.

O espectro visível pode ser dividido em subfaixas de acordo com a cor, com a subfaixa do vermelho abarcando os comprimentos de onda longos, a subfaixa do verde ao centro e a subfaixa do violeta abarcando aos comprimentos de onda mais curtos, subdivisões essas facilmente identificáveis na ilustração acima ou mesmo em um arco-íris. Os comprimentos de onda nessa faixa de radiação estão compreendidos entre 370 nm (violeta) e 750 nm (vermelho),^[1] sendo comum afirmar-se por aproximação que os comprimentos de onda dessa faixa localizam-se entre os 400 e 700 nanômetros (nm). Em termos de frequência, tem-se por correspondência que o espectro visível define-se pela banda situada entre 400 THz e 790 THz.

O espectro visível não apenas é dependente da espécie como também varia muito de uma espécie animal para a outra. Os cachorros e os gatos, por exemplo, não veem todas as cores que os humanos veem, percebendo do nosso espectro visível apenas as sub-faixas do azul à amarela. Enxergam contudo geralmente bem em preto e branco, numa nuance de cinzas. Já as cobras veem no infravermelho e as abelhas no ultravioleta, faixas para as quais somos cegos. Conforme dito, nós humanos vemos numa faixa que vai do vermelho ao violeta, passando pelo verde, o amarelo e o azul, contudo mesmo entre os humanos pode haver grandes variações quanto aos detalhes da faixa percebida. Em particular os limites do espectro ótico variam muito de espécime para espécime. Pessoas daltônicas costumam ter dificuldades em visualizar cores contidas em certas faixas do espectro.

Índice

• 1História
• 2Natureza ondulatória da luz visível
• 3Energia do fóton para a luz visível
• 4Cores do Espectro
• 5Ver também
• 6Referências
• 7Ligações externas

História

Laser visível: (violeta - 445 nm), (verde - 532 nm), (vermelho - 635 nm)

O círculo colorido de Newton, do livro Opticks de 1704, que relaciona as cores com as notas, sendo, a relação uma oitava completa.

Iluminação com três diferentes fontes; vermelha, verde e azul.

No século XVII, as explicações do espectro óptico vieram de Isaac Newton, quando ele escreveu o livro Opticks. No Século XVIII Goethe escreveu sobre espectros ópticos no seu livro Teoria das Cores. Observações anteriores foram feitas por Roger Bacon que reconheceu o espectro visível em um copo de água, quatro séculos antes de Newton descobrir que os prismas podiam separar e unir a luz branca.^[2]

Newton usou pela primeira vez a palavra espectro (latim para "aparência" ou "aparição") impresso em 1671 em uma descrição de seu experimento em óptica. A palavra "espectro" (Spktrum) foi muito utilizada para designar o fantasma Afterimage de Goethe em seu livro Teoria das cores e Schopenhauer em seu livro Sobre a Visão e as Cores. Newton observou que quando um feixe estreito de luz solar se encontra com um prisma de vidro em um ângulo, uma parte é refletida e a outra parte passa o vidro, surgindo diferentes bandas de cores. Newton hipotetizou que a luz era feitas de "corpúsculos" (partículas) de diferentes cores, e que diferentes cores se moviam com diferentes velocidades na matéria transparente, com o vermelho se movendo mais rápido que o violeta, o que resulta que o vermelho possui uma angulação (refração) menor que a do violeta ao passar pelo prisma, criando um espectro de cores

No começo do século XIX, a concepção de espectro visível ficou mais definida, como os diferentes tipos de luz fora do visível foram descobertas e caracterizadas por Willian Herschell (infravermelho) e Johann Wilhelm Ritter (ultravioleta), Thomas Young, Thomas Johann Seebeck, e outros.^[3] Young foi o primeiro a medir o comprimento de onda em diferentes cores da luz, em 1802.^[4]

A conexão entre o espectro visível e visão de cores foi explorada por Thomas Young e Hermann von Helmholtz no começo do Século XIX. Sua teoria da visão de cores corretamente propõe que o olho humano usa três distintos receptores de cores.

Natureza ondulatória da luz visível

Comportamento das ondas eletromagnéticas

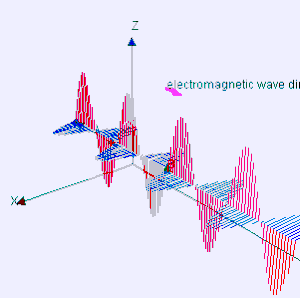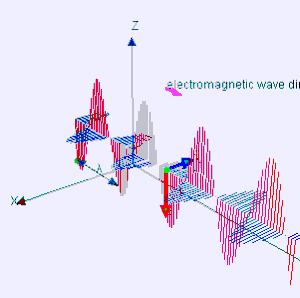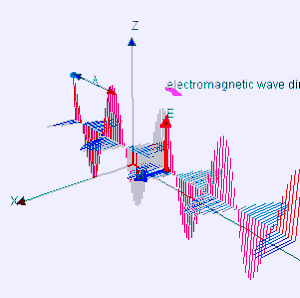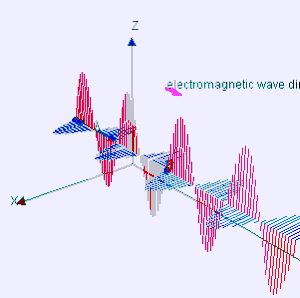
A luz que vemos com os nossos olhos é um tipo de radiação eletromagnética e fonte de energia radiante, pois transporta energia pelo espaço. Todos os tipos de radiações eletromagnéticas transportam-se no vácuo com velocidade de 3X10⁸ m/s (velocidade da luz). A radiação luminosa é periódica, isto é, o padrão de picos ou depressões repetem-se em intervalos regulares. A distancia entre dois picos ou duas depressões é chamado comprimento de onda. O tempo que a radiação emite um comprimento de onda é chamado de período da onda eletromagnética, a quantidade de períodos que são emitidos por segundo é chamado de frequência. O comprimento de onda está diretamente relacionado com a frequência. Se o comprimento de onda é longo, existirão menos ciclos da onda passando por um ponto por segundo (baixa frequência). Se há mais ciclos da onda passando por um ponto por segundo, o comprimento de onda será menor.^[5] Essa relação é dada através da equação:

${\displaystyle \eta \lambda =c}$

onde,

${\displaystyle \eta }$ é a frequência

${\displaystyle \lambda }$ é o comprimento de onda

${\displaystyle c}$ é a velocidade da luz no vácuo

Relação entre a frequência da luz e o comprimento de onda. Com uma frequência maior (violeta) se têm um comprimento de onda menor, com uma frequência menor (vermelho) se têm um comprimento de onda maior

Como a velocidade da luz é uma constante, é possível perceber a proporcionalidade da relação entre a frequência e o comprimento de onda, ou seja, quanto maior a frequência menor é o comprimento de onda e vice-versa.

Energia do fóton para a luz visível

Os fótons foram descobertos por Max Planck (1858-1947) em 1900, ele propôs que a energia podia ser liberada ou absorvida pelos átomos através de “pacotes” de energia (Planck nomeou esses “pacotes” de quantum, que significa quantidade fixa), sendo assim todo átomo absorve ou emite quantidades múltiplas de um valor fixo. Esse valor é conhecido como Constante de Planck (h), sendo sua unidade joule segundos.^[5] Em 1905, Albert Einstein (1879-1955), através da teoria de Planck pode explicar o efeito fotoelétrico.^[5] Einstein deduziu que cada fóton deveria ter proporcional a frequência da luz certa quantidade de energia, sendo assim,

${\displaystyle h=6,63\times 10^{-34}J.s}$

${\displaystyle E=h\eta }$  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Sendo :

${\displaystyle h}$ a Constante de Planck;

${\displaystyle \eta }$ a frequência;

${\displaystyle E}$ a energia do fóton.

Sendo assim, para calcularmos a energia dos fótons do espectro visível, é só multiplicar a frequência (na faixa de 400 Thz a 750 Thz) pela Constante de Planck.

Cores do Espe

Espectro da radiação de corpo negro para diversas temperaturas. A lei de Wien descreve o comportamento do comprimento de onda para o qual a intensidade da radiação é máxima em função da temperatura.

A lei de Wien (ou lei do deslocamento de Wien) é a lei da física que relaciona o comprimento de onda onde se situa a máxima emissão de radiação eletromagnética de corpo negro e sua temperatura:^[1]

${\displaystyle \lambda _{\text{max}}={\frac {b}{T}}}$ .

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Nessa expressão, ${\displaystyle \lambda _{\text{max}}\,}$ é o comprimento de onda (em metros) para o qual a intensidade da radiação eletromagnética emitida é máxima, ${\displaystyle T\,}$ é a temperatura do corpo em kelvins, e ${\displaystyle b\,}$ é a constante de proporcionalidade, chamada constante de dispersão de Wien, em m.K (metro x Kelvin).

O valor dessa constante é ${\displaystyle b=2,8977685\times 10^{-3}}$ m.K

O que resulta em:

${\displaystyle \lambda _{\text{max}}={\frac {0,0028976}{T}}}$

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Conforme a lei de Wien, quanto maior for a temperatura de um corpo negro, menor será o comprimento de onda para o qual a emissão é máxima. Por exemplo, a temperatura da fotosfera solar é de 5 780 K e o pico de emissão se produz a 475 nm =${\displaystyle (4,75\cdot 10^{-7}m)}$. Como 1 angstrom 1 Å= 10⁻¹⁰ m=10⁻⁴ µm resulta que o máximo ocorre a 4 750 Å.

Dedução

Esta lei foi formulada empiricamente por Wilhelm Wien. Entretanto, hoje se deduz da lei de Planck para a radiação de um corpo negro da seguinte maneira:

${\displaystyle E(\lambda ,T)={C_{1} \over \lambda ^{5}\cdot (e^{C_{2} \over \lambda \cdot T}-1)}={C_{1}\cdot \lambda ^{-5} \over (e^{C_{2} \over \lambda \cdot T}-1)}}$

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde as constantes valem no Sistema Internacional de Unidades:

${\displaystyle C_{1}=8\pi hc=4,99589\cdot 10^{-24}[J\cdot m]}$

${\displaystyle C_{2}={hc \over k}=1,4385\cdot 10^{-2}{m\cdot K}=1,4385\cdot 10^{4}[\mu m\cdot K]}$

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Para encontrar o máximo, a derivada da função com respeito a ${\displaystyle \lambda }$ tem de ser zero.

${\displaystyle {\partial (E(\lambda ,T)) \over \partial \lambda }=0}$

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Basta utilizar a regra de derivação do quociente e como se tem que igualar a zero, o numerador da derivada será nulo ou seja:

${\displaystyle {\frac {c_{2}}{\lambda \cdot T}}=5\cdot (1-e^{-C_{2} \over \lambda \cdot T})}$

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Se definimos

${\displaystyle x\equiv {c_{2} \over \lambda T}}$

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

então

${\displaystyle {x \over 1-e^{-x}}-5=0}$

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Esta equação não pode ser resolvida analiticamente. Utilizando o método de Newton ou da tangente:

${\displaystyle x=4.965114231744276\ldots }$

Da definição de x resulta que:

${\displaystyle \lambda _{\text{max}}\cdot T={\frac {c_{2}}{x}}={\frac {1.4385\cdot 10^{4}}{4.965114231744276}}=2897,6\mu mK}$

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Assim que a constante de Wien é ${\displaystyle 2897,6\mu m\cdot K}$ pelo que:

${\displaystyle \lambda _{\text{max}}\cdot T=2897,6\mu m\cdot K}$

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Dispersão em um raio de luz em um prisma.

Em física, uma relação de dispersão expressa a relação existente entre as frequências ${\displaystyle f}$ e o comprimento de onda ${\displaystyle \lambda }$, ou, de forma equivalente,^[1] entre as frequências ${\displaystyle f}$ e as velocidades ${\displaystyle v}$, atrelada a entes físicos de natureza ondulatória (fases) propagando-se em um dado meio material ou mesmo no vácuo. Geralmente, traduz-se mediante uma função ou um gráfico de frequência x comprimento de onda — ou de frequência x velocidade — e quase sempre mostra-se bem dependente do meio de propagação, caracterizando-o inclusive.

De forma similar mas não idêntica, um espectro discrimina a amplitude ou intensidade — o que traduz-se geralmente por quantidade de energia — das fases como função de suas respectivas frequências. Espectros e relações de dispersão encontram-se certamente relacionados, mas são por definição distintos.

Índice

• 1Óptica
• 2Mecânica
  • 2.1Relações de dispersão para o vácuo
• 3Ver também
• 4Referências
• 5Bibliografia

Óptica

A relação de dispersão influi diretamente nas trajetórias de propagação de ondas quando há mudança do meio de propagação, visto que as relações de dispersão são geralmente diferentes nos diferentes meios de propagação e que as mudanças nas direções de propagação ocorrem justamente em virtude de mudanças nos comprimentos de onda quando ondas com uma dada frequência atravessam a interface entre os diferentes meios. A dependência destas variações nas direções de propagação com a as frequências ou comprimentos de onda explicam porque a luz branca é, através de um fenômeno ótico conhecido por refração, separada em suas várias cores (frequências) ao atravessar um prisma ou mesmo gotas de água. As relações de dispersão para a onda no ar e no vidro, ou no ar e na água são bem distintas: em ambos os casos as componentes das ondas são fisicamente separadas em função de suas frequências, cada qual sofrendo um maior ou menor desvio em sua trajetória ao mudarem de meio, o que dá origem por fim aos espectros e ao arco-iris.

A relação de dispersão é importante para entender como que a energia, o momento ou mesmo a matéria são transportados de um ponto a outro em qualquer meio. O interesse na relação de dispersão provavelmente começou com o interesse na dispersão de ondas na água, como por exemplo, demostrado por Pierre-Simon Laplace em 1776.^[2]

Mecânica

Em mecânica o termo relação de dispersão refere-se à relação — normalmente uma função — que estabelece a energia que um dado ente físico possui em função do momento que este transporta. Em partículas livres no domínio da física clássica — com massas de repouso não nulas e velocidades muito inferiores à da luz — a relação de dispersão é uma função quadrática do momento: ${\displaystyle E={\frac {{\vec {P}}^{2}}{2m}}}$. Esta relação aparece de forma explícita no hamiltoniano para o sistema em questão e conduz à expressão para a energia cinética: ${\displaystyle E_{c}={\frac {1}{2}}mv^{2}}$ ao considerar-se que ${\displaystyle {\vec {P}}=m{\vec {V}}}$.  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

A relação acima vale no contexto da física clássica e para partículas completamente livres. Em situações mais específicas, como aquelas encontradas em física do estado sólido, a exemplo no estudo de elétrons confinados na estrutura dos cristais semicondutores, a relação de dispersão para as partículas — no caso os elétrons — pode mostrar-se dependente inclusive da direção de propagação das mesmos dentro do sistema. No caso do estudo dos cristais o momento para os elétrons dentro dos mesmos é definido de forma adequada à situação, sendo então denominado momento cristalino do elétron.

No âmbito da relatividade ou da mecânica quântica as expressões que definem o momento das partículas em estudo podem assumir formas também bem distintas da expressão clássica ${\displaystyle {\vec {P}}=m{\vec {v}}}$, o mesmo ocorrendo para as expressões da energia, mas em qualquer caso a relação entre o momento e a energia — ou seja, a relação de dispersão — mostra-se igualmente importante, sendo geralmente o cerne de qualquer teoria que busque estabelecer a dinâmica de matéria, energia e momento nos sistemas físicos sob seu domínio.

Em qualquer teoria dinâmica a relação de dispersão mostra-se fundamental, e a partir da mesma é que se define outras grandezas geralmente importantes ao estudo, como a massa.

A associação do termo "relação de dispersão" com a relação existente entre energia e momento para os entes físicos com massa de repouso (partículas massivas) decorre diretamente dos princípios estabelecidos por De Broglie e Max Planck no âmbito da física quântica. De Broglie trouxe à luz o fato de que partículas massivas têm comportamento ondulatório, onde seus comprimento de onda encontram—se relacionados aos seus momentos, ao passo que, sob a mesma óptica, Plank mostrou que a energias associadas às partículas quânticas encontram-se relacionadas às frequências das ondas a elas associadas. Estabelecer uma relação entre energia e momento é assim estabelecer uma relação entre frequência e comprimento de onda, ou seja, estabelecer uma relação de dispersão, mesmo para o caso de partículas massivas.

Relações de dispersão para o vácuo

Fato curioso e de relevância na mecânica quântica é que, ao passo que o vácuo é um meio não dispersivo para ondas eletromagnéticas (as assim chamadas velocidades de fase são iguais à velocidade de grupo em um pulso eletromagnético — todos com velocidades iguais à "c", a velocidade da luz), o vácuo é um meio dispersivo para ondas de matéria (funções de onda), a velocidade de fase dependendo do momento segundo a relação ^[3]:

${\displaystyle V_{\phi }={\frac {\hbar k}{(2m)}}={\frac {p}{2m}}}$ p  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Repare que a velocidade (real) esperada para a partícula não é a velocidade de fase de uma onda plana de matéria (partícula livre), mas sim a velocidade de grupo das ondas que formam o pacote de ondas associado à partícula, a velocidade de grupo obedecendo relação bem mais similar à esperada classicamente:

${\displaystyle V_{g}={\frac {\hbar k}{m}}={\frac {p}{m}}}$

onde ${\displaystyle \hbar }$ é a constante reduzida de Planck, p é o módulo do momento e k o número de onda atrelados à partícula em questão.  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

ara partículas livres (ondas de matéria planas).

Radiação de corpo negro

A Lei de Planck para radiação de corpo negro exprime a radiância espectral em função do comprimento de onda e da temperatura do corpo negro.

${\displaystyle I(\nu ,T)={\frac {2h\nu ^{3}}{c^{2}}}{\frac {1}{(e^{\frac {h\nu }{kT}}-1)}}}$

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

A tabela seguinte descreve as variáveis e unidades utilizadas:

Variável	Descrição	Unidade
${\displaystyle I\,}$	radiância espectral	J•s−1•m−2•sr−1•Hz−1
${\displaystyle \nu \,}$	frequência	hertz
${\displaystyle T\,}$	temperatura do corpo negro	kelvin
${\displaystyle h\,}$	constante de Planck	joule / hertz
${\displaystyle c\,}$	velocidade da luz no vácuo	metros / segundo
${\displaystyle e\,}$	número de Euler	sem dimensão
${\displaystyle k\,}$	constante de Boltzmann	joule / kelvin

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

O comprimento de onda está relacionado a frequência como (supondo propagação de uma onda no vácuo):

${\displaystyle \lambda ={c \over \nu }.}$

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Pode-se escrever a Lei de Planck em termos de energia espectral:

${\displaystyle u(\nu ,T)={4\pi \over c}I(\nu ,T)={\frac {8\pi h\nu ^{3}}{c^{3}}}~{\frac {1}{(e^{\frac {h\nu }{kT}}-1)}}}$v

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

A energia espectral também pode ser expressa como função do comprimento de onda:

${\displaystyle u(\lambda ,T)={8\pi hc \over \lambda ^{5}}{1 \over (e^{\frac {hc}{\lambda kT}}-1)}}$

  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Max Planck produziu esta lei em 1900 e a publicou em 1901, na tentativa de melhorar a expressão proposta por Wilhelm Wien que adequou dados experimentais para comprimentos de onda curtos desviados para comprimentos de onda maiores. Ele estabeleceu que a Lei de Planck adequava-se para todos os comprimentos de onda extraordinariamente bem. Ao deduzir esta lei, ele considerou a possibilidade da distribuição de energia eletromagnética sobre os diferentes modos de oscilação de carga na matéria. A Lei de Planck nasceu quando ele assumiu que a energia destas oscilações foi limitada para múltiplos inteiros da energia fundamental E, proporcional à freqüência de oscilação ${\displaystyle \nu }$ ^[1]:

${\displaystyle E={h\nu }}$ .  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Planck acreditava que a quantização aplicava-se apenas a pequenas oscilações em paredes com cavidades (que hoje conhecemos como átomos), e não assumindo as propriedades de propagação da Luz em pacotes discretos de energia. Além disto, Planck não atribuiu nenhum significado físico a esta suposição, mas não acreditava que fosse apenas um resultado matemático que possibilitou uma expressão para o espectro emitido pelo corpo negro a partir de dados experimentais dos comprimentos de onda. Com isto Planck pôde resolver o problema da catástrofe do ultravioleta encontrada por Rayleigh e Jeans que fazia a radiância espectral tender ao infinito quando o comprimento de onda aproximava-se de zero, o que experimentalmente não é observado. É importante observar também que para a região do visível a fórmula de Planck pode ser aplicada pela aproximação de Wien e da mesma forma para temperaturas maiores e maiores comprimentos de onda podemos ter também a aproximação dada por Rayleigh e Jeans.

Radiação síncrotron emitida por um feixe de elétrons curvado pelo campo magnético de um eletroímã.

Representação pictórica do processo de emissão de radiação por uma partícula movendo-se ao longo de geodésicas circulares ao redor de um buraco negro de Schwarzschild no espaço-tempo de de Sitter.

Radiação síncrotron, radiação sincrotrônica ^{(português brasileiro)} ou radiação sincrotrónica ^{(português europeu)} é a radiação eletromagnética emitida por uma partícula carregada (tipicamente elétrons ou pósitrons) movendo-se com velocidade relativística (ou seja, próxima à velocidade da luz) ao longo de uma trajetória curva, com raio de curvatura relativamente grande. Essa condição se aplica, em particular, para partículas circulando em aceleradores de elétrons ou pósitrons, cujo raio de curvatura é da de vários metros a dezenas de metros. O nome desta radiação deriva de um tipo específico de acelerador, o síncrotron de elétrons.^[1]

A radiação síncrotron também pode ter origem natural, sendo produzida por objetos astronômicos, como por exemplo remanescentes de supernovas (pulsares), quasares e núcleos de galáxias ativas. A radiação é produzida quando elétrons relativísticos espiralam ao longo dos campos magnéticos produzidos por estes objetos.^[2][3] Em astrofísica, uma partícula se movendo ao longo de geodésicas do espaço-tempo ao redor de buracos negros emite radiação síncrotron.^[4][5][6][7]

Jato energético da galáxia M87. A luz azul é causada por radiação síncrotron.

Índice

• 1História
• 2Potência irradiada
• 3Propriedades
• 4Aplicações
• 5Ver também
• 6Referências

História

Os primeiros trabalhos teóricos sobre a radiação emitida por elétrons em órbitas circulares foram motivados pelas tentativas de se desenvolver modelos atômicos para explicar os espectros atômicos. Porém esses trabalhos foram tornados obsoletos pelo modelo atômico de Bohr. Posteriormente, no início dos anos de 1940, o interesse no problema foi reavivado com o advento de aceleradores de elétrons circulares como o bétatron, e a constatação de que essa radiação emitida era um fator limitante na energia máxima que poderia ser alcançada com esses aceleradores.^[1]

O tratamento teórico dessa radiação foi desenvolvido por várias pessoas, entre elas destacam-se: J. Schwinger e D. Ivanenko, A.A. Solokov e I.M.Ternov^[1], além de D.H.Tomboulian e P.L. Hartman, Godwin e Jackson.^[8]

Do ponto de vista experimental, a radiação emitida por um acelerador síncrotron foi observada em 1946 nos laboratórios da General Electric. Essa observação foi feita com um síncrotron de elétrons de 70 MeV localizado em Schenectady.^[1]

Até o final dos anos de 1950, o estudo da radiação síncrotron foi motivada principalmente pelo seu aspecto negativo na tecnologia de aceleradores. Mas em 1956, um artigo de Tomboulian e Hartman, iniciou uma revolução em termos de utilização dessa radiação, eles utilizaram a radiação para estudos de espectroscopia de absorção no ultravioleta distante e raios X.^[1]

Potência irradiada

Como ponto de partida, pode-se tomar a expressão para a potência irradiada por uma carga acelerada não relativística, também conhecida como fórmula de Larmor:^[8][9]

${\displaystyle P={\frac {2}{3}}{\frac {e^{2}}{m^{2}c^{3}}}{\Bigl (}{dp \over dt}{\Bigr )}^{2}}$ (1) em unidades cgs.  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

${\displaystyle e}$ = carga elétrica;

${\displaystyle m}$ = massa;

${\displaystyle c}$ = velocidade da luz;

${\displaystyle p}$ = momento.

Para uma carga em movimento circular com o raio da órbita valendo ${\displaystyle \rho }$, temos que a potência irradiada será:

${\displaystyle P={\frac {2}{3}}{\frac {e^{2}c}{\rho ^{2}}}\beta ^{4}\gamma ^{4}}$ (2)  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

${\displaystyle \rho }$ = raio da órbita;

${\displaystyle \beta ={\frac {v}{c}}}$  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

${\displaystyle \gamma ={\frac {1}{\sqrt {1-(v^{2}/c^{2})}}}}$  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Além disso, pode-se mostrar que a energia perdida (ΔE) a cada revolução é:

${\displaystyle \Delta E={\frac {4\pi }{3}}{\frac {e^{2}}{\rho }}\beta ^{3}\gamma ^{4}}$ (3)  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Para partículas com energias relativísticas, ${\displaystyle \beta }$${\displaystyle \approxeq }$ 1, assim a equação (2) nos diz que a potência irradiada é inversamente proporcional a ${\displaystyle \rho }$² e diretamente proporcional a ${\displaystyle \gamma }$⁴.

Sendo que ${\displaystyle \gamma }$ (fator de Lorentz) pode ser escrito como:

${\displaystyle \gamma ={\frac {E_{total}}{E_{repouso}}}}$  ////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

A ${\displaystyle E_{repouso}}$ do elétron é 0,511 MeV e a do próton é 938 MeV. Assim, para a mesma energia total e o mesmo raio, pode-se notar que partículas pesadas como o próton, produzem uma intensidade de radiação síncrotron desprezível quando comparada com a que é produzida por elétrons.