- Gerar link
- X
- Outros aplicativos
O MUNDO DAS DIMENSÕES DE GRACELI
O MUNDO DAS DIMENSÕES DE GRACELI.
ONDE NÃO APENAS O ESPAÇO E O TEMPO SÃO SÃO DIMENSÕES, MAS TAMBÉM TODA FORMA DE ESTRUTURAS, ENERGIAS, CATEGORIAS, FENÔMENOS E ESTADOS FÍSICOS E QUÂNTICO E ESTADOS DE GRACELI. CONFIGURAÇÃO ELETRÔNICA , E OUTTOS
ONDE FORMAM O INFINITO-DIMENSIONAL DE GRACELI.
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.
TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.
ONDE CADA INFINITA PARTÍCULA TEM INFINITAS DIMENSÕES FORMANDO UM SISTEMA GERAL UNIFICATÓRIO COM PADRÕES DE VARIAÇÕES CONFORME AS PARTÍCULA QUE NO CASO PASSAM A REPRESENTAR DIMENSÕES, PADRÕES DE ENERGIAS E E PADRÕES POTENCIAIS DE TRANSFORMAÇÕES, INTERAÇÕES CATEGORIAS FÍSICAS DE GRACELI E OUTROS.
NA TEORIA DAS CORDAS PARTÍCULAS SÃO REPRESNTADAS POR VIBRAÇÕES.
JÁ NA TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL. NO CASO SÃO REPRENTADOS POR DIMENSÕES FÍSICAS E QUÍMICA DE GRACELI.
TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :
sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL
sistema indeterminístico Graceli ;
SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +
SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos
SISTEMA GRACELI INFINITO-DIMENSIONAL.
SISTEMA GRACELI INFINITO-DIMENSIONAL.
COM ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.
ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.
TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO E ESPECÍFICO NÍVEL DE ENERGIA.
SISTEMA MULTIDIMENSIONAL GRACELI
ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.
Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].
Em física, a conexão de Berry e a curvatura de Berry são conceitos relacionados que podem ser vistos, respectivamente, como um potencial de gauge local e um campo de gauge associado à fase de Berry ou fase geométrica.[1] Esses conceitos foram introduzidos por Michael Berry em um artigo publicado em 1984, enfatizando como as fases geométricas fornecem um poderoso conceito unificador em vários ramos da física clássica e quântica.[2]
Fase de Berry e evolução adiabática cíclica
Na mecânica quântica, a fase de Berry surge em uma evolução adiabática cíclica.[3] O teorema adiabático quântico se aplica a um sistema cujo hamiltoniano 







- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
onde o segundo termo exponencial é o "fator de fase dinâmica". O primeiro termo exponencial é o termo geométrico, com 

- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
indicando que a fase de Berry depende apenas do caminho no espaço de parâmetros, não da taxa em que o caminho é percorrido.
No caso de uma evolução cíclica em torno de um caminho fechado 

- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
Um exemplo de sistema físico em que um elétron se move ao longo de um caminho fechado é o movimento do ciclotron (detalhes são fornecidos na página da fase de Berry). A fase de baga deve ser considerada para obter a condição de quantização correta.
Proposta pelo físico estadunidense Josiah Willard Gibbs, a Regra das Fases de Gibbs apresenta um critério para a determinação das fases que coexistirão em um sistema em equilíbrio num diagrama de fase.[1]
Definição
A regra das fases de Gibbs é expressa pela equação
,
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
em que P é o número de fases presentes, F é o número de graus de liberdade, ou o número de variáveis que podem ser controladas externamente, e que devem ser especificadas para definir por completo o estado de um sistema. O parâmetro C representa o número de componentes e N é o número de variáveis não relacionadas à composição. Como muitas vezes essas variáveis são a temperatura e a pressão, é comum a equação aparecer como:
.
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
Sistema unário
Para sistemas com um só componente, em que C = 1 e as variáveis são temperatura e pressão, de modo que N = 2, a equação toma a forma
.
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
No ponto triplo coexistem três fases em equilíbrio. Como há apenas um componente, o número de graus de liberdade é dado por
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
ou seja, F = 0. Isso significa que nenhuma variável (temperatura ou pressão) pode ser mudada, mantendo-se a existência das três fases.
Ao longo de um contorno de fase, duas fases estão em equilíbrio, de modo que
Em física, termodinâmica, química, físico-química e física da matéria condensada, um ponto crítico, também chamado de estado crítico, ocorre sob condições (tais como valores específicos de temperatura, pressão ou composição) no qual não existem limites de fase. Existem vários tipos de pontos críticos, incluindo pontos críticos líquido-vapor e líquido-líquido.[1][2]
Índice
Substâncias puras: ponto crítico líquido-vapor
O "ponto crítico" é por vezes usado para denotar o ponto especificamente vapor-líquido crítico de um material, a partir do qual a distinção entre fase a líquida e gasosa não existe.
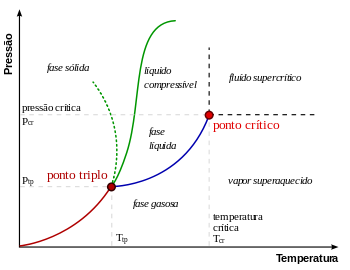
O ponto crítico de vapor-líquido em um diagrama de fases pressão-temperatura está no extremo de alta temperatura do limite de fase líquido-gás. A linha pontilhada verde mostra o comportamento anômalo da água.[3]
Como se mostra no diagrama de fases para a direita, isto é o ponto em que a fronteira entre a fase líquida e gasosa termina. Em água, o ponto crítico ocorre em cerca de 647 K. (374 ° C; 705 ° F) e 22,064 MPa (218 atm)
À medida que a substância se aproxima da temperatura crítica, as propriedades da sua fases gasosa e líquida convergem, resultando em apenas uma fase no ponto crítico: um fluido supercrítico homogêneo. O calor de vaporização é zero no ponto crítico e para além dele, por isso não existe distinção entre as duas fases. No diagrama de Pressão-temperatura, o ponto em que a temperatura crítica e pressão crítica satisfazer é chamado de ponto crítico da substância. Acima da temperatura crítica, um líquido não pode ser formada por um aumento da pressão, apesar de um sólido poder ser formado sob uma pressão suficiente. A pressão crítica é a pressão de vapor, à temperatura crítica. O volume crítico é o volume molar de uma mole do material a uma temperatura e pressão críticas.
Propriedades críticas variam de material para material, e para muitas substâncias puras estão prontamente disponíveis na literatura. No entanto, a obtenção de propriedades críticas para misturas é mais desafiador.
Definição matemática
No caso das substâncias puras, há um ponto de inflexão na curva isotérmica crítica (linha de temperatura constante) com um diagrama de Pressão-Volume. Isto significa que, no ponto crítico: [4][5][6]
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
Isto é, as primeira e segunda derivadas parciais da pressão p no que diz respeito ao volume V são ambos zero, com as derivadas parciais avaliados em temperatura constante T. Esta relação pode ser usada para avaliar dois parâmetros de uma equação de estado em termos das propriedades críticas, tais como os parâmetros a e b na equação de van der Waals.[4]
Às vezes um conjunto de propriedades reduzidas é definida em termos das propriedades importantes, isto é:[7]
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
onde 



História
A existência de um ponto crítico foi descoberto pela primeira vez por Charles Cagniard de la Tour em 1822[8] [9] e nomeado por Thomas Andrews, em 1869.[10] Ele mostrou que o CO2 poderia ser liquefeito a 31 ° C a uma pressão de 73 atm, mas não a uma temperatura ligeiramente mais elevada, mesmo sob uma pressão muito mais elevada (até 3,000 atm).
Misturas: ponto crítico líquido-líquido
O ponto crítico líquido-líquido de uma solução, o que ocorre a uma temperatura crítica da solução, ocorre no limite da região de duas fases no diagrama de fases. Em outras palavras, é o ponto no qual uma mudança infinitesimal em alguma variável termodinâmica (tais como a temperatura ou a pressão), conduzirá a separação da mistura em duas fases líquidas distintas, como se mostra no diagrama de fases do polímero-solvente à direita. Existem dois tipos de pontos críticos líquido-líquido, que são a temperatura de solução crítica superior , em inglês (UCST), representa o ponto mais quente na qual o arrefecimento irá induzir a separação de fases, e a temperatura de solução crítica inferior, em inglês (TCIS), que é o ponto mais frio no qual o aquecimento irá induzir a separação de fases.
Definição matemática
Do ponto de vista teórico, o ponto crítico líquido-líquido representa o extremo da temperatura da concentração da curva spinodal (como pode ser visto na figura, à direita). Assim, o ponto crítico líquido-líquido em um sistema de dois componentes deve satisfazer duas condições: condição da curva spinodal (a segunda derivada da energia livre em relação a concentração deve ser igual a zero), e da condição extrema (a terceira derivada da energia livre no que diz respeito à concentração também deve ser igual a zero ou a derivada da temperatura spinodal com respeito à concentração deve ser igual a zero).
Fluido supercrítico é qualquer substância em uma temperatura e pressão acima do seu ponto crítico, no qual não existe mais distinção entre as fases líquida e gasosa. Ele sofre efusão através de sólidos como um gás, e pode dissolver materiais como um líquido. Além disso, perto do seu ponto crítico, pequenas mudanças em sua pressão ou temperatura resultam em grandes mudanças de densidade, permitindo que sejam feitos pequenos ajustes nas propriedades de um fluido supercrítico.
Os fluidos supercríticos são substitutos adequados a solventes orgânicos em uma variedade de processos industriais e laboratoriais. Dióxido de Carbono e água são os fluidos supercríticos mais comumente usados, para descafeinação e geração de eletricidade, respectivamente.
Índice
Propriedades
Em termos gerais, fluidos supercríticos tem propriedades entre a de um gás e a de um líquido. Na Tabela 1, as propriedades críticas de alguns componentes que são comumente usados como fluidos supercríticos são mostradas.
| Solvente | Peso molecular | Temperatura Crítica | Pressão Crítica | Densidade Crítica |
|---|---|---|---|---|
| g/mol | K | MPa (atm) | g/cm3 | |
| Dióxido de Carbono (CO2) | 44.01 | 304.1 | 7.38 (72.8) | 0.469 |
| Água (H2O) | 18.015 | 647.096 | 22.064 (217.755) | 0.322 |
| Metano (CH4) | 16.04 | 190.4 | 4.60 (45.4) | 0.162 |
| Etano (C2H6) | 30.07 | 305.3 | 4.87 (48.1) | 0.203 |
| Propano (C3H8) | 44.09 | 369.8 | 4.25 (41.9) | 0.217 |
| Etileno (C2H4) | 28.05 | 282.4 | 5.04 (49.7) | 0.215 |
| Propileno (C3H6) | 42.08 | 364.9 | 4.60 (45.4) | 0.232 |
| Metanol (CH3OH) | 32.04 | 512.6 | 8.09 (79.8) | 0.272 |
| Etanol (C2H5OH) | 46.07 | 513.9 | 6.14 (60.6) | 0.276 |
| Acetona (C3H6O) | 58.08 | 508.1 | 4.70 (46.4) | 0.278 |
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
A Tabela 2 mostra densidade, coeficiente de difusão e viscosidade para gases, líquidos e fluidos supercríticos típicos.
| Densidade (kg/m3) | Viscosidade (µPa∙s) | Coeficiente de difusão (mm²/s) | |
|---|---|---|---|
| Gases | 1 | 10 | 1–10 |
| Fluidos supercríticos | 100–1000 | 50–100 | 0.01–0.1 |
| Líquidos | 1000 | 500–1000 | 0.001 |
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
Além disso, não há tensão superficial em um fluido supercrítico, já que não há uma divisão entre as fases líquida e gasosa. Mudando a pressão e temperatura do fluido, as propriedades podem ser ajustadas para serem mais parecidas com as de um líquido ou de um gás. Uma das mais importantes propriedades é a solubilidade do material no fluido. Solubilidade num fluido supercrítico tende a aumentar com a densidade do fluido (a uma temperatura constante). Já que a densidade aumenta com a pressão, a solubilidade tende a aumentar com a pressão. A relação com a temperatura é mais complicada. À uma densidade constante, a solubilidade irá aumentar com a temperatura, no entanto, perto do ponto crítico, a densidade pode cair abruptamente com um pequeno aumento de temperatura. Portanto, perto da temperatura crítica, a solubilidade geralmente cai com um aumento de temperatura e então cresce de novo.[2]
Todos os fluidos supercríticos são completamente miscíveis uns com os outros, então para uma mistura uma única fase pode ser garantida se o seu ponto crítico for excedido. O ponto crítico de uma mistura de dois elementos pode ser estimada através da média aritmética das temperaturas e pressões críticas dos dois componentes.[3]
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
onde:
e
são as frações molares dos componente A e B e,
e :
são suas respectivas Temperaturas Críticas.
Para uma maior precisão, o ponto crítico pode ser calculado usando equações de estado, como as de Peng Robinson, ou métodos de contribuição de grupo. Outras propriedades, como a densidade, podem ser calculadas usando equações de estado.
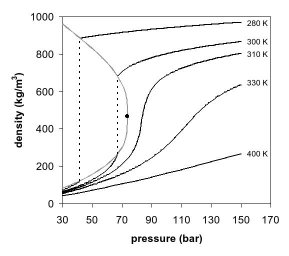
Diagrama de fase
As figuras 1 e 2 mostram projeções de diagramas de fase. No diagrama de fase de pressão por temperatura (Fig. 1) as fases líquida e gasosa são separadas pela ebulição até o ponto crítico, onde essas duas fases somem e viram uma única fase supercrítica. Isso pode ser observado no diagrama de fase de pressão por densidade do dióxido de carbono, como mostra a Figura 2. Bem abaixo da temperatura crítica, como, por exemplo, à 280K, conforme a pressão aumenta, o gás é comprimido e eventualmente, a apenas 40 bar, condensa em um líquido muito mais denso, resultando na descontinuidade na linha (linha vertical pontilhada). O sistema consiste de duas fases em equilíbrio, um líquido de alta densidade e um gás de baixa densidade. Conforme se chega próximo à temperatura crítica (300K), a densidade do gás em equilíbrio se torna maior e a do líquido menor. No ponto crítico, (304.1 K e 7.38 MPa (73.8 bar)) não há diferença na densidade, e as duas fases se tornam uma única fase fluida. Portanto, acima da temperatura crítica, um gás não pode ser liquefeito através de pressão. Um pouco acima da temperatura crítica (310K), nas proximidades da pressão crítica, a linha é quase vertical. Um pequeno incremento na pressão causa um grande aumento na densidade da fase supercrítica. Muitas outras propriedades física também mostram grandes gradientes com a pressão perto do ponto crítico, como por exemplo, a viscosidade, a constante dielétrica e a força do solvente, que são intimamente relacionados com a densidade. Em temperaturas mais altas, o fluido começa a se comportar como um gás, como pode ser visto na Figura 2. Para o dióxido de carbono, a 400K, a densidade aumenta quase linearmente com a pressão.
Muitos gases pressurizados são na verdade fluidos supercríticos. Por exemplo, o Nitrogênio tem um ponto crítico de 126.2K (-147 °C) e 3.4 MPa (34 bar). Portanto, Nitrogênio (ou ar comprimido) em um cilindro de gás acima dessa temperatura é na verdade um fluido supercrítico. Estes são mais comumente conhecidos como gases permanentes. Em temperatura ambiente, eles estão bem acima de sua temperatura crítica, e portanto se comportam como um gás, como o CO2 a 400K e acima. No entanto, eles não podem ser liquefeitos por pressão a não ser que sejam resfriados abaixo de sua temperatura crítica.
Ocorrências Naturais
Vulcões submarinos
Vulcões submarinos são comuns no fundo oceânico. Alguns são ativos e, em águas rasas, mostram sua presença através de um jato de vapor e detritos muito acima da superfície do mar. Muitos outros ficam em profundidades tão grandes que a imensa pressão do peso da água sobre eles previne esses jatos explosivos de vapor e gases. Isso faz com que a água seja aquecida a mais de 375 °C, transformando a água nas partes mais quentes do vulcão em um fluido supercrítico, já que a pressão numa profundidade de 3 km é de mais de 300 atmosferas, bem acima das 218 atmosferas necessárias.
Atmosferas planetárias
A atmosfera de Vênus é 96.5% dióxido de carbono e 3.5% Nitrogênio. A pressão na sua superfície é de 9.3 MPa (93 bar) e a temperatura é de 735K, acima dos pontos críticos dos seus principais constituintes e fazendo a superfície de sua atmosfera um fluido supercrítico.
As atmosferas interiores dos gigantes gasosos do Sistema Solar são compostas principalmente de Hidrogênio e Hélio a temperaturas muito acima de seus pontos críticos. As atmosferas gasosas exteriores de Júpiter e Saturno se transicionam suavemente até o interior fluido dos planetas. Modelos teoréticos dos planetas extra solares 55 Cancri e e Gliese 876 d postularam um oceano de água pressurizada e supercrítica com uma camada de gelo sólido a uma alta pressão no fundo.

Na física e na ciência dos materiais, a Temperatura de Curie (Tc), ou a temperatura no Ponto de Curie, é a temperatura na qual o magnetismo permanente de um material se torna um magnetismo induzido. A força do magnetismo é determinada pelo momento magnético.
A temperatura de Curie é o ponto crítico onde o momento magnético intrínseco do material muda de direção. Momentos magnéticos são momentos de dipolo permanentes que dentro do átomo são criados a partir do momento angular e do spin dos elétrons. Materiais tem diferentes estruturas de momentos magnéticos intrínsecos que variam com a mudança de temperatura.
Magnetismo permanente é causado pelo alinhamento dos momentos magnéticos e magnetismo induzido é criado quando momentos magnéticos desordenados são forçados a se alinhar em um campo magnético requerido. Por exemplo, os momentos magnéticos ordenados (ferromagnético, Figura 1) mudam e se tornam desordenados (paramagnético, Figura 2) na Temperatura de Curie.
Altas temperaturas fazem a magnetização espontânea de imãs mais fracos ocorrer apenas na Temperatura de Curie. Susceptibilidade magnética só ocorre acima da Temperatura de Curie e pode ser calculada pela Lei de Curie-Weiss que é derivada da Lei de Curie.
Em analogia aos materiais ferromagnéticos e paramagnéticos, a temperatura de Curie pode ser usada para descrever a temperatura onde polarização eletrostática espontânea do material se torna um polarização eletrostática induzida ou o contrário caso a temperatura seja reduzida abaixo da Temperatura de Curie.
A Temperatura de Curie recebeu esse nome depois que Pierre Curie mostrou que o magnetismo se perde depois de alcançar uma temperatura crítica.[1]
| Material | Temperatura de Curie (°C) |
|---|---|
| Ferro (Fe) | 770 |
| Cobalto (Co) | 1127 |
| Níquel (Ni) | 354 |
| Gadolínio (Gd) | 19 |
| Disprósio (Dy) | -185 |
| MnBi | 357 |
| MnSb | 314 |
| CrO2 | 113 |
| MnAs | 45 |
| EuO | -204 |
| Óxido férrico (Fe2O3) | 675 |
| Óxido de ferro(II,III) (FeOFe2O3) | 585 |
| NiOFe2O3 | 585 |
| CuOFe2O3 | 455 |
| MgOFe2O3 | 440 |
| MnOFe2O3 | 300 |
| Y3Fe5O12 | 287 |
| Ímã de neodímio | 310-400 |
| Alnico | 700-860 |
| Imã Samário-Cobre | 720-800 |
| Ferrite | 450 |
Índice
Lei de Curie-Weiss
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
A Lei de Curie-Weiss é uma versão adaptada da Lei de Curie.
A Lei de Curie-Weiss é um modelo simples derivado da aproximação do campo médio, isso significa que
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
funciona bem quando a temperatura do material,T, é muito maior que sua correspondente Temperatura de Curie,Tc, logo T >> Tc; Entretanto falha para descrever a susceptibilidade magnética, χ, na proximidade imediata do ponto de Curie por causa das flutuações locais entre os átomos.[5]
Ambas Lei de Curie e Lei de Curie-Weiss não servem quando T< Tc.
Lei de Curie para material paramagnético:[6]
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
| Definition | |
|---|---|
| χ | a susceptibilidade magnética; influência de um campo magnético requerido no material |
| M | momento magnético por unidade de volume |
| H | o campo magnético macroscópico |
| B | o campo magnético |
| C | a Constante Curie específica do material |
Aplicações
Em termodinâmica, o ponto triplo é um estado particular de uma substância determinado por valores de temperatura e pressão, no qual as três fases ou estados físicos da substância (sólido, líquido e gasoso) coexistem em equilíbrio.[1]
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
O ponto triplo do dióxido de carbono (CO2), por exemplo, ocorre na temperatura de 216,55 K e à pressão de 517 kPa. Já o ponto triplo do mercúrio ocorre à temperatura de −38,83440 °C e à pressão de 0,2 mPa.
Além do ponto triplo entre sólido, líquido e gasoso, podem existir pontos triplos envolvendo mais de uma fase sólida, nas substâncias com polimorfismo. Em geral, para um sistema com p fases possíveis, existem
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
pontos triplos.[1]
Note que a pressão aqui referida é a pressão de vapor da substância — não a pressão total do sistema.
O ponto triplo da água é dado por definição - não por uma medição exata. É usado para definir o kelvin, a unidade de temperatura termodinâmica no Sistema Internacional de Unidades.[2][3] Os pontos triplos de várias substâncias são usados para definir pontos na Escala Internacional de Temperaturas de 1990 (ITS-90), que vai desde o ponto triplo do hidrogênio (13,8033 K) até o ponto triplo da água (273,16 K, 0,01 °C ou 32,018 °F)
Índice
Pontos triplos da água
Ponto triplo sólido-líquido-gás
A única combinação de pressão e temperatura na qual os três estados físicos da água (sólido (gelo), gasoso (vapor) e líquido) podem coexistir em equilíbrio estável ocorre exatamente quando a temperatura é de 273,16 kelvins (0,01 °C) e a pressão é de 611,73 pascals (cerca de 0,006 bar; 0,0060373 atm). Nesse ponto, é possível mudar toda a substância para gelo, água ou vapor fazendo pequenas mudanças na temperatura e pressão.
O ponto triplo sólido-líquido-gás corresponde à mínima pressão na qual a água líquida pode existir. Sob pressões abaixo do ponto triplo (como no espaço sideral), o gelo, quando aquecido a uma pressão constante, converte-se diretamente em vapor de água, num processo conhecido como sublimação. Acima do ponto triplo, o gelo, quando aquecido a uma pressão constante, primeiro derrete, formando água líquida, e depois evapora ou ferve, passando ao estado gasoso (vapor).
Para a maioria das substâncias, o ponto triplo também é a mínima temperatura na qual o líquido pode existir. Para a água, porém, isto não é verdade, por causa de seu comportamento anômalo[4] que faz com que o ponto de fusão do gelo diminua com o aumento da pressão, conforme mostra a linha verde pontilhada, no diagrama de fases (ver figura). A uma temperatura um pouco abaixo do ponto triplo (entre 251–273 K), a compressão a temperatura constante transforma o vapor de água, primeiro, em gelo I e depois em água líquida (o gelo tem uma densidade menor do que a água líquida, de modo que um aumento de pressão leva à liquefação).
Durante a missão Mariner 9, da NASA, para Marte, a pressão do ponto triplo da água foi usada como ponto de referência para o "nível do mar". Missões mais recentes utilizam altimetria a laser e medições da gravidade, em vez da pressão, para definir elevações em Marte.[5]
Outros pontos triplos da água em pressões mais altas
Em altas temperaturas, a água tem um diagrama de fases complexo com quinze fases conhecidas do gelo e um número de pontos triplos, incluíndo os dez cujas coordenadas são mostradas no diagrama. Por exemplo, o ponto triplo em 251 K (-22 °C) e 210 MPa (2070 atm) corresponde às condições de coexistência do gelo Ih (gelo comum), gelo III e água líquida, todos em equilíbrio. Mas podem existir também pontos em que três fases sólidas coexistam em equilíbrio, como a 218 K e 620 MPa.
Células do ponto triplo
Células do ponto triplo são usadas na calibração de termômetros. Para medições exatas, células de ponto triplo são geralmente preenchidas com uma substância química com alta pureza, como o hidrogênio, argônio, mercúrio ou água, dependendo da temperatura desejada. A pureza destas substâncias pode ser tal que apenas uma parte em um milhão seja um contaminante, o que significa 99,9999% puro. As células de ponto triplo são tão eficientes no alcance de temperaturas precisas e reproduzíveis que um padrão internacional de calibração de termômetros chamado ITS-90 se baseia em células de hidrogênio, neon, oxigênio, argônio, mercúrio e água para determinar seus seis pontos definidos de temperatura.
Tabela de pontos triplos
Esta tabela lista o ponto triplo sólido-líquido-gasoso de substâncias comuns. A menos que diferentemente indicadas, as informações vieram da U.S. National Bureau of Standars (agora NIST (National Institute of Standards and Technology).[6]
| Substância | T [K] | p [kPa]* |
|---|---|---|
| Acetileno | 192,4 | 120 |
| Amoníaco | 195,40 | 6,076 |
| Argônio | 83,81 | 68,9 |
| Arsênio | 1090 | 3628 |
| Butano | 134,6 | 7 × 10−4 |
| Carbono (grafite) | 4765 | 10132 |
| Dióxido de carbono | 216,55 | 517 |
| Monóxido de carbono | 68,10 | 15,37 |
| Clorofórmio | 175,43 | 0,870 |
| Deuterio | 18,63 | 17,1 |
| Etano | 89,89 | 8 × 10−4 |
| Etanol | 150 | 4,3 × 10−7 |
| Etileno | 104,0 | 0,12 |
| Ácido fórmico | 281,40 | 2,2 |
| Hélio-4 (ponto lambda) | 2,19 | 5,1 |
| Hexafluoroetano | 173,08 | 26,60 |
| Hidrogênio | 13,84 | 7,04 |
| Cloreto de Hidrogênio | 158,96 | 13,9 |
| Iodo[7] | 386,65 | 12,07 |
| Isobutano[8] | 113,55 | 1,9481 × 10−5 |
| Mercúrio | 234,2 | 1,65 × 10−7 |
| Metano | 90,68 | 11,7 |
| Neon | 24,57 | 43,2 |
| Óxido nítrico | 109,50 | 21,92 |
| Nitrogênio | 63,18 | 12,6 |
| Óxido nitroso | 182,34 | 87,85 |
| Oxigênio | 54,36 | 0,152 |
| Paládio | 1825 | 3,5 × 10−3 |
| Platina | 2045 | 2,0 × 10−4 |
| Dióxido de enxofre | 197,69 | 1,67 |
| Titânio | 1941 | 5,3 × 10−3 |
| Hexafluoreto de urânio | 337,17 | 151,7 |
| Água | 273,16 | 0,6117 |
| Xenônio | 161,3 | 81,5 |
| Zinco | 692,65 | 0,065 |
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
* Nota: Para fins de comparação, a pressão atmosférica típica é 101,325 kPa (1 atm).
Quando um líquido composto por dois ou mais componentes é aquecido, o ponto de bolha é a temperatura (a uma dada pressão) onde a primeira bolha de vapor é formada. Dado que o vapor, provavelmente, terá uma composição diferente do líquido o ponto de bolha (junto com o ponto de orvalho) em diferentes composições são dados úteis no projeto de sistemas de destilação (como em refinarias de petróleo).
Para um único componente, o ponto de bolha e o ponto de orvalho são os mesmos e são referidos como o ponto de ebulição.
Calculando o ponto de bolha
Em um ponto de bolha, as seguintes relações mantem-se:
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
onde
.
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
K é o coeficiante de distribuição ou fator K, definido como a razão da fração molar na fase de vapor 

Quando a lei de Raoult e lei de Dalton sustentam-se para a mistura, o fator K é definido como a razão entre a pressão de vapor à pressão total do sistema:[1]
- ////
TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.
- Gerar link
- X
- Outros aplicativos












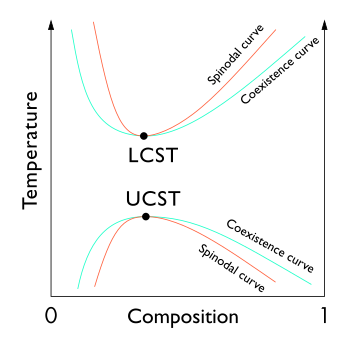









Comentários
Postar um comentário