O MUNDO DAS DIMENSÕES DE GRACELI

 

O MUNDO DAS DIMENSÕES DE GRACELI

novembro 16, 2021

 O MUNDO DAS DIMENSÕES DE GRACELI.

ONDE NÃO APENAS O ESPAÇO E O TEMPO SÃO SÃO DIMENSÕES, MAS TAMBÉM TODA FORMA DE ESTRUTURAS, ENERGIAS, CATEGORIAS, FENÔMENOS E ESTADOS FÍSICOS E QUÂNTICO E ESTADOS DE GRACELI. CONFIGURAÇÃO ELETRÔNICA , E OUTTOS

ONDE FORMAM O INFINITO-DIMENSIONAL DE GRACELI.

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

novembro 06, 2021

 TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

outubro 27, 2021

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

ONDE CADA INFINITA PARTÍCULA TEM INFINITAS DIMENSÕES FORMANDO UM SISTEMA GERAL UNIFICATÓRIO COM PADRÕES DE VARIAÇÕES CONFORME AS PARTÍCULA QUE NO CASO PASSAM A REPRESENTAR DIMENSÕES, PADRÕES DE ENERGIAS E E PADRÕES POTENCIAIS DE TRANSFORMAÇÕES, INTERAÇÕES CATEGORIAS FÍSICAS DE GRACELI E OUTROS.

NA TEORIA DAS CORDAS PARTÍCULAS SÃO REPRESNTADAS POR VIBRAÇÕES.

JÁ NA TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL. NO CASO SÃO REPRENTADOS POR DIMENSÕES FÍSICAS E QUÍMICA DE GRACELI.

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL

setembro 20, 2021

 sistema indeterminístico Graceli ;

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

 SISTEMA GRACELI INFINITO-DIMENSIONAL.

COM  ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.

ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.

  TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA.

SISTEMA MULTIDIMENSIONAL  GRACELI

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].

DENTRO DE UMA CONCEPÇÃO QUE CADA ÁTOMO É FORMADO DE INFINITAs OUTRAS PARTÍCULAS, E COM INFINITAS OUTRAS ENERGIAS, INTERAÇÕES, TRANSFORMAÇÕES, E OUTROS FENÔMENOS, LOGO SE TEM EM CADA ÁTOMO E OU ELEMENTO QUÍMICO INFINITAS OUTRAS DIMENSÕES. COM INFINITAS VARIAÇÕES NAS CATEGORIAS DE GRACELI , QUE  SÃO: OS POTENCIAIS, TIPOS, NÍVEIS, E TEMPO DE AÇÃO ESPECÍFICO  DO FENÔMENO.

ONDE NOS SISTEMAS  DE GRACELI CATEGORIAS,  FENÔMENOS, ESTADOS, ENERGIAS, ESTRUTURAS, E OUTROS SÃO TIPOS E FORMAS DE DIMENSÕES..

FLUXOS ALEATÓRIOS DE ENERGIAS ELÉTRICA,  E FLUXOS DE SALTOS QUÂNTICOS INFINITESIMAIS E INDETERMINADOS.

SENDO QUE VARIAM CONFORME O SISTEMA INFINITO-DIMENSIONAL.

O SISTEMA INFINITO-DIMENSIONAL DE GRACELI, ASSIM, COMO O SISTEMA SDCTIE GRACELI [SISTEMA ENVOLVENDO DIMENSÕES DE GRACELI, E SUAS CATEGORIAS, ESTADOS FÍSICOS E ESTADOS FÍSICOS DE GRACELI, TRANSFORMAÇÕES E INTERAÇÕES], E OS TENSORES DE GRACELI TEM AÇÃO EM TODA A FÍSICA EM TODOS OS SEUS RAMOS E E DIVISÕES, ASSIM, COMO A QUÍMICA E A BIOLOGIA, QUE TODOS ESTES SE FUNDAMENTEM EM ENERGIAS, ONDAS, ESTRUTURAS, CATEGORIAS, ESTADOS, ESPECTROS, DIMENSÕES, E OUTROS.

OU SEJA, DENTRO DE UM SISTEMA GERAL DE GRACELI TODA FÍSICA DAS ESTRTURUAS, ENERGIAS, ONDAS, DIMENSÕES, ESTADOS, E CATEGORIAS. ESTÃO INSERIDOS NESTES SISTEMA DE GRACELI.

dentro de uma concepção que a matéria é infinitésima em termos de tipos e ínfimos diâmetro, logo esta diferenciação faz com que cada ínfima e infinitésima parte tenha ações, transformações, interaçõs, potenciaidades, e outros diferentes de uma das outras. logo se tem infinitas dimensões para cada ínfima e infinitésima parte e tipo.

VEJAMOS;

MECÂNICA, ASTRONOMIA   E FÍSICA GRACELI ANGULAR .

CONFORME O ÂNGULO  DE INCIDÊNCIA  SE TEM VARIAÇÕES DOS FENÔMENOS , ISTO EM TODA AS FÍSICAS ASTRONOMIA E OUTROS FENÔMENOS.

COMO NO EFEITO FOTOELÉTRICO, ATMOSFERAS, AURORAS, E OUTROS FENÕMENOS.

A termodinâmica quântica é o estudo das relações entre duas teorias físicas independentes: termodinâmica e mecânica quântica.^[1][2] As duas teorias independentes tratam dos fenômenos físicos da luz e da matéria. Em 1905, Einstein argumentou que a exigência de consistência entre termodinâmica e eletromagnetismo^[3] nos leva à conclusão de que a luz é quantizada obtendo a relação ${\displaystyle E=h\nu }$. Este artigo é o início da teoria quântica. Em algumas décadas, a teoria quântica se estabeleceu com um conjunto independente de regras.^[4] Atualmente, a termodinâmica quântica trata do surgimento de leis termodinâmicas da mecânica quântica. Ela difere da mecânica estatística quântica na ênfase em processos dinâmicos fora de equilíbrio.^[5] Além disso, há uma busca pela teoria para ser relevante para um único sistema quântico individual.^[6]

Visualização dinâmica

Existe uma conexão íntima da termodinâmica quântica com a teoria dos sistemas quânticos abertos.^[7] A mecânica quântica insere dinâmica na termodinâmica, dando uma base sólida à termodinâmica para tempo finito. A principal premissa é que o mundo inteiro é um grande sistema fechado e, portanto, a evolução do tempo é governada por uma transformação unitária gerada por um hamiltoniano global. Para o cenário combinado do banho do sistema, o Hamiltoniano global pode ser decomposto em:

${\displaystyle H=H_{S}+H_{B}+H_{SB}}$

///////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde ${\displaystyle H_{S}}$ é o sistema hamiltoniano, ${\displaystyle H_{B}}$ é o banho hamiltoniano e${\displaystyle H_{SB}}$ é a interação sistema-banho. O estado do sistema é obtido a partir de um rastreamento parcial sobre o sistema combinado e o banho: ${\displaystyle \rho _{S}(t)=Tr_{B}(\rho _{SB}(t))}$. Dinâmica reduzida é uma descrição equivalente da dinâmica do sistema, utilizando apenas operadores do sistema. Assumindo a propriedade de Markov para a dinâmica, a equação básica de movimento para um sistema quântico aberto é a equação de Lindblad (GKLS):^[8][9]

${\displaystyle {\dot {\rho }}_{S}=-{i \over \hbar }[H_{S},\rho _{S}]+L_{D}(\rho _{S})}$

///////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

${\displaystyle H_{S}}$ é uma parte hamiltoniana (Hermitiana) e ${\displaystyle L_{D}}$:

${\displaystyle L_{D}(\rho _{S})=\sum _{n}\left(V_{n}\rho _{S}V_{n}^{\dagger }-{\frac {1}{2}}\left(\rho _{S}V_{n}^{\dagger }V_{n}+V_{n}^{\dagger }V_{n}\rho _{S}\right)\right)}$

///////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

é a parte dissipativa que descreve implicitamente através dos operadores do sistema ${\displaystyle V_{n}}$ a influência do banho no sistema. A propriedade de Markov impõe que o sistema e o banho não estejam correlacionados o tempo todo ${\displaystyle \rho _{SB}=\rho _{s}\otimes \rho _{B}}$. A equação L-GKS é unidirecional e conduz qualquer estado inicial ${\displaystyle \rho _{S}}$ para uma solução em estado estacionário que é invariável da equação do movimento ${\displaystyle {\dot {\rho }}_{S}(t\rightarrow \infty )=0}$.^[7]

A imagem de Heisenberg fornece uma ligação direta para observáveis termodinâmicos quânticos. A dinâmica de um sistema observável representado pelo operador, ${\displaystyle O}$, tem a forma:

${\displaystyle {\frac {dO}{dt}}={\frac {i}{\hbar }}[H_{S},O]+L_{D}^{*}(O)+{\frac {\partial O}{\partial t}}}$

///////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde a possibilidade de que o operador, ${\displaystyle O}$ é explicitamente dependente do tempo, está incluído.

O condensado de Bose-Einstein é uma fase da matéria formada por bósons a uma temperatura muito próxima do zero absoluto. Nestas condições, uma grande fracção de átomos atinge o mais baixo estado quântico, e nestas condições os efeitos quânticos podem ser observados à escala macroscópica. A existência deste estado da matéria como consequência da mecânica quântica foi inicialmente prevista por Albert Einstein em 1925, no seguimento do trabalho efetuado por Satyendra Nath Bose. O primeiro condensado deste tipo foi produzido setenta anos mais tarde por Eric Cornell e Carl Wieman em 1995, na Universidade do Colorado em Boulder, usando um gás de átomos de rubídio arrefecido a 170 nK (nano Kelvin).^[1]

Dados de distribuição de velocidade confirmando a descoberta de um novo estado da matéria, o Condensado de Bose-Einstein, a partir de um gás de Rubídio

• 10Ligações externas

Descrição detalhada do gráfico de distribuição de velocidades

As cores artificiais representam o número de átomos em cada velocidade, indicando o vermelho menos átomos e o branco mais átomos. As áreas em que aparecem branco e azul claro são velocidades menores. Esquerda: Logo antes do aparecimento do condensado de Bose-Einstein. Centro: No instante do aparecimento do condensado. Direita: após a rápida evaporação, deixando amostras puras do condensado. O pico não é infinitamente estreito devido ao Princípio da Incerteza de Heisenberg: quando um átomo é retido numa região específica do espaço a sua distribuição de velocidade possui necessariamente uma certa largura mínima.

Introdução

Os condensados de Bose-Einstein são fluidos de temperaturas baixas com propriedades não totalmente compreendidas, como fluir espontaneamente para fora do seu recipiente. Este efeito é uma consequência da mecânica quântica, que postula que qualquer sistema só pode adquirir energia em quantidades discretas. Se um sistema está a uma temperatura tão baixa que esteja no seu estado de energia mínima, não é possível reduzir a sua energia, nem sequer por fricção. Assim sendo, sem fricção, o fluido facilmente supera a gravidade devido às forças de adesão entre o fluido e a parede do seu recipiente e tomará a posição mais favorável, ou seja, a toda a volta do recipiente.

Teoria

O abrandamento de átomos por meio de arrefecimento produz um estado quântico único conhecido como condensado de Bose ou condensado de Bose-Einstein. Este fenômeno foi teorizado nos anos 20 por Albert Einstein, ao generalizar o trabalho de Satyendra Nath Bose sobre a mecânica estatística dos Fótons (sem massa) para átomos (com massa). (O manuscrito de Einstein, que se pensava estar perdido, foi encontrado em 2005 numa biblioteca da Universidade de Leiden). O resultado do trabalho de Bose e Einstein é o conceito de gás de Bose, governado pela estatística de Bose-Einstein que descreve a distribuição estatística de partículas idênticas de spin inteiro, conhecidas hoje em dia como Bósons. As partículas bosónicas, que incluem o Fóton e átomos como o He-4, podem partilhar estados quânticos umas com as outras. Einstein especulou que arrefecendo os átomos bosónicos até temperaturas muito baixas os faria colapsar (ou "condensar") para o mais baixo estado quântico acessível, resultando numa nova forma de matéria.

Esta transição ocorre abaixo de uma temperatura crítica, a qual, para um gás tridimensional uniforme consistindo em partículas não-interactivas e sem graus internos de liberdade aparentes, é dada por:

${\displaystyle T_{c}=\left({\frac {n}{\zeta (3/2)}}\right)^{2/3}{\frac {h^{2}}{2\pi mk_{B}}}}$

///////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde:

${\displaystyle T_{c}}$	é	a temperatura crítica,
${\displaystyle n}$		a densidade da partícula,
${\displaystyle m}$		a massa por bóson,
${\displaystyle h}$		a constante de Planck,
${\displaystyle k_{B}}$		a constante de Boltzmann, e
${\displaystyle \zeta }$		a função zeta de Riemann; ${\displaystyle \zeta (3/2)}$ ≈ 2,6124. Em física estatística e física da matéria condensada, densidade de estados (DOS, do inglês density of states) é a propriedade que quantifica quão proximamente "empacotado" em níveis de energia está um sistema mecânico quântico. Um DOS alto em um nível específico de energia significa que há muitos estados disponíveis para ocupação. Um DOS nulo, zero, significa que nenhum estado pode ser ocupado em um nível de energia. 5Ligações externas Explanação Ondas, partículas comportando-se como ondas, podem somente existir dentro de sistemas mecânico quânticos (MQ) se propriedades do sistema seguem a ondulação existente. Em alguns sistemas, o espaçamento interatômico e a carga atômica do material segue somente elétrons de certos comprimento de onda existentes. Em outros sistemas. a estrutura cristalina do material leva ondas a se propagar em somente uma direção, enquanto suprime a propagação de ondas em outra direção. Ondas em um sistema MQ tem comprimentos de onda específicos e podem propagar-se em direções específicas, e cada onda ocupa um diferente modo,ou estado. Devido a muitos destes estados terem o mesmos comprimentos de onda, entretanto dividirem a mesma energia, podem existir muitos estados disponíveis em certos níveis de energia, enquanto nenhum estado é disponível em outros níveis de energia. Por exemplo, a densidade de estados para elétrons em um semicondutor é mostrada em vermelho na Fig. 2. Para elétrons na fronteira da faixa de condução, muito poucos estados estão disponíveis para o elétron ocupar. A medida que o elétron aumenta em energia, a densidade de estados do elétron aumenta e mais estados tornam-se disponíveis para ocupação. Entretanto, porque não há estados disponíveis para elétrons ocuparem dentro da faixa de abertura, elétrons na fronteira da faixa de condução devem perder pelo menos ${\displaystyle E_{g}}$ de energia de maneira a realizarem a transição a outro estado disponível. A densidade de estados pode ser calculada para elétrons, fótons, ou fónons em sistemas MQ. É usualmente notado com um dos símbolos g, ${\displaystyle \rho }$, n, ou N. É uma função g(E) da energia interna E, na qual a expressão g(E) dE representa o número de estado com energias entre E e E+dE. Para converter entre energia e vetor de onda, a relação específica entre E e k deve ser conhecida. Por exemplo, a fórmula para elétrons é ${\displaystyle E={\frac {(\hbar k)^{2}}{2m}}}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. E para fótons, a fórmula é ${\displaystyle E=\hbar ck}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. Pode também ser escrito como uma função da frequência angular ${\displaystyle \omega }$, a qual é proporcional à energia. A densidade de estados é usada extensivamente em física da matéria condensada, onde pode referir-se ao nível de energia dos elétrons, fótons ou fônons em um sólido cristalino. Em sólidos cristalinos, há frequentemente níveis de energia onde a densidade dos estados dos elétrons é zero, o que significa que os elétrons não podem ser excitados a estas energias. A densidade dos estados também ocorre na regra dourada de Fermi, a qual descreve quão rápido as transições mecânico quânticas ocorrem na presença de uma perturbação. Num sistema tridimensional, a densidade de estados em espaço recíproco (espaço k) é ${\displaystyle G(k)\,dk={\frac {nV}{2\pi ^{2}}}\,k^{2}\,dk,}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. onde V é o volume e n o número de pontos de ramificação que existem para um único valor de k. Estes pontos de ramificação são por exemplo o spin-acima e spin-abaixo estados para elétrons, as polarizações de fótons, e os modos longitudinais ou transversais para fônons. Materiais cristalinos Dado que em materiais (cristalinos), o número de escalas varia linearmente com o volume, uma diferente definição de densidade de estados é algumas vezes usada, na qual g(E) ou g(k) é o número de estados por unidade de energia (vetor onda) e por unidade de volume ou por unidade de célula da grade. Em um material cristalino, onde os estados mecânico quânticos podem ser descritos em termos de seus vetores de onda k, a densidade dos estados como uma função de k é não dependente das propriedades do material. Das condições periódicas segue que em um volume arbitrário ${\displaystyle V=L^{3}}$, somente vetores k são mantidos satisfazendo ${\displaystyle (k_{x},k_{y},k_{z})={\frac {2\pi }{L}}(n_{x},n_{y},n_{z}),}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. onde ${\displaystyle n_{i}}$ são inteiros positivos ou negativos arbitrários. Usando ${\displaystyle |k|^{2}=k_{x}^{2}+k_{y}^{2}+k_{z}^{2},}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. pode ser derivado que para uma matriz tridimensional o número de estados G(k) dk entre k e k+dk é ${\displaystyle G(k)={\frac {Vk^{2}}{2\pi ^{2}}}}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. para um único caso. Em sólidos, a relação entre E e k é geralmente muito complexa e dependente do material. Se a relação é conhecida, a expressão para a densidade dos estados é ${\displaystyle g(E)=G(k(E)){\frac {dk}{dE}}.}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. A relação acima é somente significativa se a energia somente depende da manitude ${\displaystyle |k|}$ do vetor k. Chama-se acoplamento vibrónico ou acoplamento electrão-fonão à interação entre estados electrónicos e estados vibratórios (ou fonões). Também é chamado efeito pseudo-Jahn-Teller, pela sua relação conceptual com o conhecido efeito Jahn-Teller.[1][2] Este acoplamento tem consequências perceptíveis nas propriedades ópticas, magnéticas e de localização-deslocalização electrónica na molécula. Opticamente, a banda de intervalência que apresentam os compostos de valência mista torna-se mais complexa e adquire uma estrutura pelo acoplamento vibrónico.[3] Também o acoplamento magnético é afectado, se existem electrões desemparelhados no sistema. Dependendo do tipo de acoplamento vibrónico que predomine, a deslocalização electrónica pode ser intensificada o diminuída[4] Definição O acoplamento vibrônico descreve a mistura de estados electrónicos diferentes como um resultado de pequenas vibrações. ${\displaystyle \mathbf {f} _{k'k}\equiv \langle \,\chi _{k'}(\mathbf {r} ;\mathbf {R} )\,|\,{\hat {\nabla }}_{\mathbf {R} }\chi _{k}(\mathbf {r} ;\mathbf {R} )\rangle _{(\mathbf {r} )}}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. O efeito Hall está relacionado ao surgimento de uma diferença de potencial em um condutor elétrico, transversal ao fluxo de corrente e um campo magnético perpendicular à corrente. Esse fenômeno foi descoberto em 1879 por Edwin Herbert Hall,[1] e é extremamente importante no estudo da condutividade, pois a partir do coeficiente de Hall é possível determinar o sinal e a densidade de portadores de carga em diferentes tipos de materiais. O efeito Hall é a base de diversos métodos experimentais utilizados na caracterização de metais e semicondutores. 7Ligações externas Descoberta Em 1879 Edwin Herbert Hall descobriu o efeito que leva seu nome durante seu doutorado em física sob a supervisão de Henry Augustus Rowland na Universidade Johns Hopkins em Baltimore, Maryland. Durante seus estudos experimentais sobre a influência do campo magnético nos portadores de carga da corrente elétrica ele determinou a existência de portadores de carga negativa muitos anos antes da descoberta dos elétrons por Joseph John Thomson. Ele descobriu que um campo magnético desviaria o movimento de cargas eletrônicas dentro de um condutor e que a quantidade de deflexão pode ser medida como uma voltagem perpendicular ao fluxo de carga, essa voltagem também é conhecida como voltagem Hall, que revela as informações essenciais sobre os portadores de carga em um semicondutor, incluindo se são elétrons negativos ou quase partículas positivas, sua velocidade em um campo elétrico ou sua “mobilidade” (µ) e sua densidade (n) dentro do semicondutor.[2] Teoria Durante seus estudos de doutorado, Edwin Hall buscava entender qual a influência de um campo magnético externo sob um fio condutor. Ele queria entender se a força devido a este campo externo atuaria sobre os portadores de corrente elétrica ou sobre o fio como um todo. Hall acreditava que essa força magnética atuaria sobre os portadores de carga fazendo com que a corrente se deslocasse para uma determinada região do fio, e portanto, a resistência do fio iria aumentar. Apesar de não observar tal aumento na resistência do fio em seus experimentos, Hall sabia que de alguma forma a corrente elétrica era alterada sem que a resistência fosse modificada. Ele propôs a presença de um estado de stress em uma determinada região do condutor, devido ao acúmulo de portadores de carga, que originaria uma diferença de potencial transversal mais tarde conhecida como tensão de Hall. Para entender melhor a origem desse fenômeno vamos considerar a definição para corrente elétrica segundo o modelo de Drude, ou seja, vamos considerar que a corrente é formada por um fluxo de portadores de carga (elétrons, íons ou lacunas) que seguem uma trajetória linear até que se choquem com os átomos da rede, impurezas, fônons, etc. Em seus experimentos, Hall considerou um fio metálico conduzindo corrente elétrica ao longo do eixo x (com densidade de corrente ${\displaystyle \mathbf {j} _{x}}$), sob a ação de um campo magnético externo ${\displaystyle \mathbf {B} }$ aplicado ao longo do eixo z. A presença do campo faz com que os portadores de carga experimentem uma força magnética que causa uma deflexão na trajetória dos portadores na direção y. Essa mudança de trajetória gera um gradiente de cargas e consequentemente surge um campo elétrico na direção y ${\displaystyle \mathbf {E} _{y}}$, conhecido como campo de Hall. Devido as dimensões finitas do fio haverá um acúmulo de cargas nas extremidades ao longo da direção y, resultando em uma diferença de potencial conhecida como potencial de Hall, ${\displaystyle V_{H}}$. Para um metal simples, ou seja, com um único portador de carga, o potencial de Hall pode ser escrito como: ${\displaystyle V_{H}={\frac {-IB}{nqd}}}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. Onde ${\displaystyle n}$ representa a densidade de portadores e ${\displaystyle d}$ a espessura do fio. Uma outra quantidade interessante relacionada ao efeito Hall é o coeficiente de Hall, que é a constante de proporcionalidade entre o campo de Hall e o produto do campo magnético com o fluxo de corrente ${\displaystyle R_{H}={\frac {\mathbf {E} _{y}}{\mathbf {B} \mathbf {j} _{x}}}={\frac {dV_{H}}{IB}}={\frac {-1}{nq}}}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. Como o sinal da força magnética é o mesmo para cargas positivas se movendo em uma determinada direção e cargas negativas se movendo na direção oposta, o sinal do coeficiente de Hall depende exclusivamente do campo de Hall. Assim, como o sinal de ${\displaystyle \mathbf {E} _{y}}$ depende exclusivamente do sinal da carga dos portadores, o coeficiente de Hall permite identificar se o fluxo de corrente se deve a portadores negativos (${\displaystyle R_{H}<0}$) ou positivos (${\displaystyle R_{H}>0}$). Desta maneira, podemos concluir que o efeito Hall, além de permitir a determinação da densidade de corrente e a mobilidade dos portadores ou do campo magnético, este também permite a distinção entre um fluxo de cargas positivas e negativas. O efeito Hall é a primeira prova real de que a corrente elétrica em metais se deve ao movimento dos elétrons e não dos prótons. Ainda mais, esse efeito demonstrou que em alguns materiais, especialmente semicondutores do tipo p, a maneira mais apropriada de se descrever a corrente elétrica é através do fluxo de buracos positivos ao invés de elétrons. Contudo, o efeito Hall gera confusões em alguns casos, por exemplo, buracos se movendo para a esquerda na realidade são elétrons se movendo para a direita e portanto devemos ter o mesmo sinal para o coeficiente de Hall, o que não ocorre. Tal problema só pode ser solucionado quando consideramos a teoria quântica do transporte em sólidos [2]. Efeito Hall em semicondutores A forma do coeficiente de Hall para semicondutores é mais complexa, uma vez que podemos ter dois tipos de portadores de carga, elétrons e buracos, com densidades e mobilidades diferentes. Para o caso de campos magnéticos moderados podemos escrever o coeficiente de Hall como sendo [3] ${\displaystyle R_{H}={\frac {-n\mu _{e}^{2}+p\mu _{b}^{2}}{e(n\mu _{e}+p\mu _{b})}}}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. onde ${\displaystyle n}$ e ${\displaystyle p}$ são as densidades e ${\displaystyle \mu _{e}}$ e ${\displaystyle \mu _{b}}$ são as mobilidades para os elétrons e buracos respectivamente. No caso de campos magnéticos altos o coeficiente de Hall é análogo ao caso de um único portador ${\displaystyle R_{H}={\frac {-(p-nb^{2})}{e(p+nb)^{2}}}}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. onde ${\displaystyle b=\mu _{e}/\mu _{b}}$. Efeito Hall quântico Ver artigo principal: Quantum Hall Effect (em inglês) Efeito observado em sistemas eletrônicos de duas dimensões sob baixas temperaturas e altos campos magnéticos. A característica marcante desse efeito é a presença de uma condutividade de Hall quantizada, onde a quantização esta relacionada aos níveis de Landau. Efeito Hall com spin Ver artigo principal: Spin Hall Effect (em inglês) O efeito Hall com spin esta relacionado com a existência de um acúmulo de spin nas extremidades de um condutor com uma corrente de portadores. Neste caso, não é necessária a presença de um campo magnético externo para se observar o efeito. Esse efeito foi descoberto por I. Dyakonov e V.I.Perel, em 1971, e observado experimentalmente 30 anos mais tarde em semicondutores e metais sob criogenia e à temperatura ambiente. Efeito Hall quântico com spin Ver artigo principal: Quantum Spin Hall Effect (em inglês) Observados em semicondutores de duas dimensões onde ocorre o acoplamento spin-órbita. Efeito Hall anômalo Em materiais ferromagnéticos (e materiais paramagnéticos na presença de um campo magnético), a resistividade Hall inclui uma contribuição adicional ao efeito Hall comum, conhecido como o efeito Hall anômalo. Esse efeito depende diretamente da magnetização do material, e é frequentemente maior que o efeito Hall comum. Embora este seja um fenômeno bem conhecido, ainda existem discussões sobre sua origem em diversos materiais. O efeito Hall anômalo pode ser um efeito extrínseco causado pelo espalhamento dos portadores de carga com spin, ou um efeito intrínseco que pode ser descrito em termos do efeito de Fase de Berry no espaço dos momentum do cristal [5]. Efeito Hall em gases ionizados O efeito Hall em um gás ionizado (plasma) é significativamente diferente do efeito Hall em sólidos (onde o coeficiente de Hall ${\displaystyle R_{H}}$ é sempre muito inferior à unidade). Em um plasma, o coeficiente de Hall pode assumir qualquer valor. O coeficiente de Hall, em um plasma é a relação entre a girofrequência do elétron, ${\displaystyle \Omega _{e}}$, e a frequência de colisão entre os elétrons e as partículas pesadas ${\displaystyle \nu }$, ${\displaystyle R_{H}={\frac {\Omega _{e}}{\nu }}={\frac {eB}{m_{e}\nu }}}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. onde ${\displaystyle m_{e}}$ é a massa do elétron. O valor do coeficiente de Hall é diretamente proporcional à intensidade do campo magnético. Fisicamente, sabemos que a trajetória dos elétrons é curvadas pela força magnética. No entanto, quando o coeficiente de Hall é baixo, o movimento entre os duas colisões com as partículas pesadas é quase linear. Mas, se o coeficiente de Hall é alto, a trajetória dos elétrons é altamente curvada. No caso do gás ionizado o vetor densidade de corrente não é mais colinear ao vetor campo elétrico, e o ângulo ${\displaystyle \theta }$ entre eles esta relacionado ao coeficiente de Hall da seguinte maneira ${\displaystyle R_{H}=\cos {(\theta )}}$. /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. O efeito Mössbauer é um fenômeno descoberto pelo físico alemão Rudolf Mössbauer em 1957. Envolve emissão ressonante e sem recuo e absorção de fótons de radiação gama por átomos ligados em uma estrutura sólida e forma a base da espectroscopia Mössbauer. Índice 1História 2Descrição 3Ver também 4Referências 5Leitura adicional História A emissão e absorção de raios X por gases já havia sido observada anteriormente e esperava-se que um fenômeno similar fosse encontrado para os raios gama, que são produzidos em transições nucleares, diferentemente dos raios X, que são produzidos por transições eletrônicas. De qualquer modo, tentativas de observar ressonância de raios gama em gases falharam devido às perdas de energia por recuo, o que impede que haja ressonância (o efeito Doppler também amplia o espectro gama). Mössbauer conseguiu observar ressonância em irídio sólido, o que levantou a questão: por que a ressonância de raios gama era possível em sólidos, mas não em gases? Mössbauer propôs que, no caso de átomos ligados em uma forma sólida, sob certas circunstâncias uma fração dos eventos nucleares podem ocorrer essencialmente sem recuo. Ele atribuiu a ressonância observada a esta fração sem recuo dos eventos nucleares. Esta descoberta foi premiada com o prêmio Nobel de Física em 1961, juntamente com a pesquisa de Robert Hofstadter sobre a dispersão de elétrons no núcleo atômico. Descrição Em geral, raios gama são produzidos por transições nucleares de um estado instável de alta energia para um estado estável de baixa energia. A energia dos raios gama emitidos corresponde à energia da transição nuclear, menos uma quantidade de energia que é perdida como recuo ao átomo emissor. Se a energia de recuo perdida é pequena quando comparada com a largura de linha espectral da transição nuclear, então a energia dos raios gama ainda corresponde à energia da transição, e os raios podem ser absorvidos por um segundo átomo do mesmo tipo do primeiro. Esta emissão e subsequente absorção é chamada ressonância. Um adicional de energia de recuo é perdido durante a absorção, então para que a ressonância ocorra a energia de recuo deve ser menos da metade da largura de linha da transição. A quantidade de energia no corpo recuante (ER) pode ser deduzido da conservação do momentum: ${\displaystyle |P_{R}|=|P_{\gamma }|\,}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. ${\displaystyle |P_{R}|^{2}=|P_{\gamma }|^{2}\,}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. onde PR é o momentum da matéria recuante, e Pγ é o momentum do raio gama. Substituindo energia na equação: ${\displaystyle 2ME_{R}={\frac {E_{\gamma }^{2}}{c^{2}}}}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. ${\displaystyle E_{R}={\frac {E_{\gamma }^{2}}{2Mc^{2}}}={\frac {(\hbar k)^{2}}{2M}}}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. onde ER (=0.002 eV para 57Fe) é a energia perdida no recuo, Eγ é a energia do raio gama (=14.4 keV para 57Fe), M (=56,9354 u para 57Fe) é a massa do corpo absorvedor, e c é a velocidade da luz.[1] No caso de um gás os corpos emissores e absorvedores são átomos, então a massa é um tanto pequena, resultando em uma grande energia de recuo, impossibilitando a ressonância. (Note que a mesma equação se aplica para perdas por recuo em raios X, mas a energia do fóton é muito menor, implicando em uma perda de energia menor, que é o motivo da ressonância em fase gasosa poder ser observada com os raios X.) Em um sólido, os núcleos estão ligados à rede e não recuam da mesma forma como em um gás. A rede recua como um todo mas a energia de recuo é desprezível por causa do M na equação acima ser a massa da rede inteira. De qualquer forma, a energia em uma emissão pode ser suportada ou suprida pelas vibrações da rede. A energia dessas vibrações é quantizada em unidades conhecidas como fônons. O efeito Mössbauer ocorre porque há uma possibilidade finita de uma emissão envolver fônons. assim, em uma fração dos eventos nucleares (a fração livre de recuo, dada pelo fator Lamb-Mössbauer), o cristal inteiro se comporta como corpo recuante, e esses eventos são essencialmente livres de recuo. Nesses casos, desde que a energia de recuo seja desprezível, os raios gama emitidos tem a energia apropriada e a ressonância pode ocorrer. Em geral (dependendo da meia-vida da emissão), raios gama possuem linhas espectrais muito finas. Isto significa que são muito sensíveis a pequenas variações na energia das transições nucleares. De fato, raios gama são usados como medidor para observar os efeitos das interações entre um núcleo e seus elétrons e os elétrons das vizinhanças. Essa é a base da espectroscopia Mössbauer, que combina o efeito Mössbauer com o efeito Doppler para monitorar tais interações. Ver também A Energia de Fermi é a energia do nível ocupado mais energético em um sistema quântico fermiônico à temperatura de zero absoluto. A definição estende-se também a sistemas acima do zero absoluto, caso em que a energia de fermi corresponde à energia obtida mediante uma média das energias dos níveis quânticos com probabilidade de ocupação - devido à agitação térmica - diferentes da unidade, cada qual ponderado pela respectiva probabilidade de ocupação. Associa-se via de regra à energia de fermi a notação EF, e a nomenclatura retrata nítida homenagem ao físico ítalo-americano Enrico Fermi. 6Bibliografia 7Ver também Introdução Contexto geral A energia de Fermi é importante na hora de entender o comportamento de partículas fermiônicas, como por exemplo os elétrons. Os férmions são partículas de spin semi-inteiro para as quais verifica-se a validade do princípio de exclusão de Pauli - que dita que dois férmions idênticos não podem ocupar simultaneamente o mesmo estado quântico. Desta maneira, quando um sistema possui vários elétrons, estes ocuparão níveis de energia maiores a medida que os níveis inferiores estejam preenchidos. A energia de Fermi é um conceito que tem muitas aplicações na teoria dos orbitais atômicos, no comportamento dos semicondutores e na física do estado sólido em geral. Em física do estado sólido a superficie de Fermi é a superficie no espaço de momentos na qual a energia de excitação total se iguala à energia de Fermi. Esta superfície pode ter uma topologia não trivial. Simplificadamente se pode dizer que a superfície de Fermi divide os estados electrônicos ocupados dos que permanecem livres. Enrico Fermi e Paul Dirac, derivaram as estatísticas de Fermi-Dirac. Estas estatísticas permitem predizer o comportamento de sistemas formados por um grande número de elétrons, especialmente em corpos sólidos. A energia de Fermi de um gás de Fermi (ou gás de elétrons livres) não relativista tridimensional se pode relacionar com o potencial químico através da equação: ${\displaystyle \mu =\epsilon _{F}\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {kT}{\epsilon _{F}}}\right)^{2}+{\frac {\pi ^{4}}{80}}\left({\frac {kT}{\epsilon _{F}}}\right)^{4}+...\right]}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. onde εF é a energia de Fermi, k é a constante de Boltzmann e T é a temperatura. Portanto, o potencial químico é aproximadamente igual a a energia de Fermi à temperaturas muito inferiores a uma energia característica denominada Temperatura de Fermi, εF/k. Esta temperatura característica é da ordem de 105K para um metal a uma temperatura ambiente de (300 K), pelo que a energia de Fermi e o potencial químico são essencialmente equivalentes. Este é um detalhe significativo dado que o potencial químico, e não a energia de Fermi, é quem aparece nas estatísticas de Fermi-Dirac. Contexto avançado Principais energias em estrutura de bandas para sólidos cristalinos. 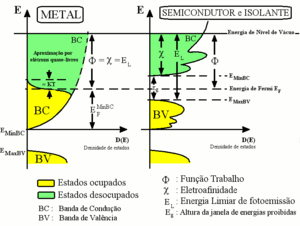Elétrons são férmions, ou seja, são partículas regidas pela estatística de Fermi. Nesta estatística, um dado estado quântico pode ser ocupado por no máximo um e não mais que um férmion, e portanto a máxima probabilidade de ocupação de um dado estado quântico é um. Os elétrons situados dentro da amostra estão confinados por um potencial atrativo exercido pelos íons positivos da rede. Conforme mostrado pela mecânica quântica, potenciais confinantes apresentam níveis de energias discretos. No caso dos átomos isto se reflete nos tão conhecidos níveis atômicos de energia e no caso dos sólidos cristalinos, a aproximação entre os átomos leva a um agrupamento dos estados em bandas de energia. Estas bandas são vistas nas relações de dispersão para os sólidos como sendo as regiões de energia permitidas para os elétrons, separadas umas das outras por janelas de energias proibidas (ou “gaps”). Rigorosamente falando,[1] a energia do nível de Fermi é definida em sistemas à temperatura de zero absoluto. Nesse caso, a energia do nível de Fermi é a energia do nível mais energético ocupado, visto que nessa temperatura todos os níveis com energia menor que a energia do nível de Fermi estariam ocupados (probabilidade igual a 1) e todos os níveis com energia acima, desocupados (probabilidade de ocupação nula). Para sistemas em temperaturas não nulas, não temos mais uma transição abrupta da probabilidade de ocupação, e sim uma probabilidade dada pela distribuição de Fermi-Dirac. Considera-se então como a energia do nível de Fermi a energia obtida pela média aritmética ponderada das energias de cada estado energético afetado pela excitação térmica (estados com probabilidades de ocupação diferentes de 1 ou 0) pesadas cada qual pela respectiva probabilidade de ocupação do estado associado. O denominador desta média será obviamente o número de estados envolvidos no processo. Repare que em acordo com a estatística de Fermi, dentre os referidos estados os menos energéticos têm probabilidade de ocupação maior do que aqueles mais energéticos. Para aproximação de elétrons livres a densidade de estados cresce com a raiz quadrada da energia, resultando em uma parábola no gráfico de energia x densidade de estados. Em semicondutores e isolantes esta dependência pode ser bem mais complicada. Outra definição equivalente implica dizer que a energia de Fermi corresponde ao potencial eletroquímico do sistema na temperatura de zero absoluto. Uma extensão a temperaturas maiores é evidente, e a energia de Fermi corresponde assim ao potencial eletroquímico do sistema na temperatura considerada. A energia de Fermi expressa, portanto, qual seria a variação da energia interna total do sólido, considerado sempre como sistema isolado e em equilíbrio termodinâmico, caso um elétron fosse dele removido. Sendo ENtotal a energia total do sistema no estado neutro, em seu equilíbrio termodinâmico, e EN-1total a energia total do sistema também em seu novo equilíbrio termodinâmico mas após a remoção do elétron, temos que: EF = ENtotal - EN-1total /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. Nas definições acima, o nível de referência é o nível de menor energia disponível aos N elétrons, e a remoção de um elétron provoca, então, a redução da energia do sistema. Neste referencial a energia de Fermi é, portanto, positiva, bem como o potencial eletroquímico. Quando dois materiais diferentes são colocados em contato, a condição de equilíbrio termodinâmico exige que as suas energias de Fermi sejam iguais. Se as energias de Fermi fossem diferentes, a passagem de um elétron do sólido com maior energia de Fermi para o sólido com menor energia de Fermi resultaria em uma diminuição da energia total do sistema e o sistema composto não estaria, então, em sua configuração de equilíbrio, a de mínima energia, conforme exigido pelas leis da termodinâmica. Este fato dá origem a um fenômeno conhecido por diferença de potencial de contato que encontra diversas aplicações práticas, a saber na eletrônica de estado sólido (junção PN) e no uso do metal de sacrifício em navios. Ilustração do conceito para compartimento monodimensional quadrado A monodimensional compartimento quadrado infinito é um modelo para uma caixa mono dimensional. É um sitema modelo padrão em mecânica quântica para o qual a solução para uma partícula isolada é bem conhecido. Os níveis são marcados por um único número quântico n e as energias são dadas por ${\displaystyle E_{n}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n^{2}\,}$. /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. Suponha-se agora que em vez de uma partícula nesta caixa nós temos N partículas na caixa e que estas partículas são férmions com spin 1/2. Então somente duas partículas podem ter a mesma energia i.e. duas partículas podem ter a energia de ${\displaystyle E_{1}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}}$, ${\displaystyle E_{f}=E_{N/2}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}(N/2)^{2}\,}$. O caso tridimensional O caso tridimensional isotrópico é conhecido como a esfera de Fermi. Deixe-nos agora considerar uma caixa cúbica tridimensional que tem um lado de comprimento L (ver compartimento quadrado infinito). Este torna-se uma muito boa aproximação para descrever elétrons em um metal. Os estados agora são marcados po três números quânticos nx, ny, e nz. As energias da partícula isolada são ${\displaystyle E_{n_{x},n_{y},n_{z}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}\right)\,}$ nx, ny, nz são inteiros positivos. Existem múltiplos estados com a mesma energia, por exemplo ${\displaystyle E_{100}=E_{010}=E_{001}}$. Agora deixemos colocar-se N férmions não interativos de spin 1/2 nesta caixa. Para calcular a energia de Fermi, nós veremos no caso de que N é grande. Se nós introduzios um vetor ${\displaystyle {\vec {n}}=\{n_{x},n_{y},n_{z}\}}$ então cada estado quântico corresponde a um ponto num "n-espaço" com energia ${\displaystyle E_{\vec {n}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}|{\vec {n}}|^{2}\,}$. O número de estados com energia menor que Ef é igual ao número de estados que residem em uma esfera de raio ${\displaystyle |{\vec {n}}_{f}|}$ na região do "n-espaço" onde nx, ny, nz são positivos. No estado básico este número iguala o número de férmions no sistema. ${\displaystyle N=2\times {\frac {1}{8}}\times {\frac {4}{3}}\pi n_{f}^{3}\,}$ Os três férmions que ocupam os mais baixos estados de energia formam uma esfera em espaço de momento. A superfície desta esfera é a superfície de Fermi. o fator é de dois é novamente porque são doisestados de spin, o fator de 1/8 é porque somente 1/8 da esfera repousa na região onde todos n são positivos. Nós obtemos ${\displaystyle n_{f}=\left({\frac {3N}{\pi }}\right)^{1/3}}$ então a energia de Fermi é dada por ${\displaystyle E_{f}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n_{f}^{2}}$ ${\displaystyle ={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{2/3}}$ Tais resultados em uma relação entre a energia de Fermi e o número de partículas por volume (quando nós substituímos L2 com V2/3): ${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m}}\left({\frac {3\pi ^{2}N}{V}}\right)^{2/3}\,}$ A energia de Fermi total de um esfera de fermi de ${\displaystyle N_{0}}$ férmions é dada por ${\displaystyle E_{t}={\int _{0}}^{N_{0}}E_{f}(N)dN={3 \over 5}N_{0}E_{f}}$ ${\displaystyle E_{t}={\int _{0}}^{N_{0}}E_{f}(N)dN={\int _{0}}^{N_{0}}{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{\frac {2}{3}}dN}$ ${\displaystyle ={\frac {3^{\frac {2}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{2mL^{2}}}{\int _{0}}^{N_{0}}N^{\frac {2}{3}}dN={\frac {3^{\frac {2}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{2mL^{2}}}\left({\frac {3}{5}}N_{0}^{\frac {5}{3}}\right)={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$ Energia de Fermi total: ${\displaystyle E_{t}={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$ Integração por substituição: ${\displaystyle E_{t}={\frac {3}{5}}N_{0}E_{f}={\frac {3}{5}}N_{0}\left[{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N_{0}}{\pi }}\right)^{2/3}\right]={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$ ${\displaystyle E_{t}={\frac {3}{5}}N_{0}E_{f}}$ A eliminação de ${\displaystyle L}$ em favor de ${\displaystyle V}$: ${\displaystyle L^{2}=V^{\frac {2}{3}}}$ ${\displaystyle E_{t}={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}N_{0}^{\frac {5}{3}}}{10mV_{0}^{\frac {2}{3}}}}}$ Energias de Fermi típicas Anãs brancas Estrelas conhecidas como anãs brancas tem massa comparável a nosso Sol, mas têm um raio aproximadamente 100 vezes menor. As alta densidades implicam que os elétrons estão não mais ligados a um núcleo isolado e formam um gás de elétrons degenerado. Os números da densidade de elétrons em uma anã branca são da ordem de 1036 elétrons/m3. Isto significa que sua energia de Fermi é: ${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m_{e}}}\left({\frac {3\pi ^{2}(10^{36})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 3\times 10^{5}\ \mathrm {eV} \,}$ Núcleos Outro exemplo típico é as partículas em um núcleo de um átomo. Os núcleons de um núcleo atômico pode ser tratado, assim, como um gás de Fermi e como tal, modelado.[2] O raio do núcleo é aproximadamente[3]: ${\displaystyle R=\left(1.25\times 10^{-15}\mathrm {m} \right)\times A^{1/3}}$ onde A é o número de núcleons. O número densidade de núcleons em um núcleo é conseqüentemente: ${\displaystyle n={\frac {A}{{\begin{matrix}{\frac {4}{3}}\end{matrix}}\pi R^{3}}}\approx 1.2\times 10^{44}\ \mathrm {m} ^{-3}}$ Agora, como a energia de fermi somente aplica-se a férmions de mesmo tipo, deve-se dividir esta energia por dois. Isto por causa da presença de nêutrons que não afetam a energia de Fermi dos prótons no núcleo, e vice versa.[4][5][6] Assim a energia de fermi de um núcleo é dada por: ${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m_{p}}}\left({\frac {3\pi ^{2}(6\times 10^{43})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 30\times 10^{6}\ \mathrm {eV} =30\ \mathrm {MeV} }$ O raio do núcleo admite desvios em torno do valor mencionado acima, então um típico valor para a energia de Fermi normalmente dada é 38 MeV. Referências /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.  ou duas partículas podem ter energia ${\displaystyle E_{2}=4E_{1}}$ e assim por diante. A razão que duas partículas podem ter a mesma energia é que uma partícula de spin 1/2 pode ter um spin de 1/2 (spin "acima") ou um spin de -1/2 (spin "abaixo"), conduzindo a dois estadois para cada nível de energia. Quando nós olhamos na energia total deste sistema, a configuração para as quais a energia total é a menor (o estado fundamental), é a configuração onde todos os níveis de energia acima de n=N/2 estão ocupados e todos os níveis mais altos estão vazios. A energia de Fermi é consequentemente A flexoeletricidade é uma propriedade de um material dielétrico, pelo qual exibe uma polarização elétrica espontânea induzida por um gradiente de deformação.[1] A flexoeletricidade está intimamente relacionada à piezoeletricidade, mas enquanto a piezoeletricidade se refere à polarização devido à tensão uniforme, a flexoeletricidade se refere especificamente à polarização devido à tensão que muda de um ponto para outro no material.[2] Flexoeletricidade não é o mesmo que Ferroelasticidade[3]. A polarização elétrica devido ao estresse mecânico em um dielétrico é dada por: ${\displaystyle P_{i}=d_{ijk}\sigma _{jk}+\mu _{ijkl}{\frac {\partial \epsilon _{jk}}{\partial x_{l}}}}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. onde o primeiro termo corresponde ao efeito piezoelétrico direto e o segundo termo corresponde à polarização flexoelétrica induzida pelo gradiente de deformação. Aqui, o coeficiente flexoelétrico, ${\displaystyle \mu _{ijkl}}$, é um tensor polar de quarta ordem e ${\displaystyle d_{ijk}}$ é o coeficiente correspondente ao efeito piezoelétrico direto. O efeito fotoelétrico é a emissão de elétrons por um material, geralmente metálico, quando exposto a uma radiação eletromagnética (como a luz) de frequência suficientemente alta, que depende do material, como por exemplo a radiação ultravioleta. Ele pode ser observado quando a luz incide numa placa de metal, arrancando elétrons da placa. Os elétrons ejetados são denominados fotoelétrons.[1] Observado pela primeira vez por A. E. Becquerel em 1839 e confirmado por Heinrich Hertz em 1887,[2] o fenômeno é também conhecido por "efeito Hertz",[3][4] não sendo porém este termo de uso comum, mas descrito pela primeira vez por Albert Einstein, o efeito fotoelétrico explica como a luz de alta frequência libera elétrons de um material.[5] De acordo com a teoria eletromagnética clássica, o efeito fotoelétrico poderia ser atribuído à transferência de energia da luz para um elétron. Nessa perspectiva, uma alteração na intensidade da luz induziria mudanças na energia cinética dos elétrons emitidos do metal. Além disso, de acordo com essa teoria, seria esperado que uma luz suficientemente fraca mostrasse um intervalo de tempo entre o brilho inicial de sua luz e a emissão subsequente de um elétron. No entanto, os resultados experimentais não se correlacionaram com nenhuma das duas previsões feitas pela teoria clássica. Em vez disso, os elétrons são desalojados apenas pelo impacto dos fótons quando esses fótons atingem ou excedem uma frequência limite (energia). Abaixo desse limite, nenhum elétron é emitido do material, independentemente da intensidade da luz ou do tempo de exposição à luz (raramente, um elétron irá escapar absorvendo dois ou mais quanta; no entanto, isso é extremamente raro porque ao absorver quanta suficiente para escapar, o elétron provavelmente terá emitido o resto dos quanta absorvidos). Para dar sentido ao fato de que a luz pode ejetar elétrons mesmo que sua intensidade seja baixa, Albert Einstein propôs que um feixe de luz não é uma onda que se propaga através do espaço, mas uma coleção de pacotes de ondas discretas (fótons), cada um com energia. Isso esclareceu a descoberta anterior de Max Planck da relação de Planck (E = hν), ligando energia (E) e frequência (ν) como decorrentes da quantização de energia. O fator h é conhecido como a constante de Planck.[6][7][1] Em 1921 o alemão Albert Einstein recebeu o prêmio Nobel de Física por "suas contribuições para a física teórica e, especialmente, por sua descoberta da lei do efeito fotoelétrico."[8] Índice 1Descrição 2Equações 3Aplicações 4Ver também 5Referências Descrição Tomemos um exemplo: a luz vermelha de baixa frequência estimula os elétrons para fora de uma peça de metal; na visão clássica, a luz é uma onda contínua cuja energia está espalhada sobre a onda. Todavia, quando a luz fica mais intensa, mais elétrons são ejetados, contradizendo, assim a visão da física clássica que sugere que os mesmos deveriam se mover mais rápido (energia cinética) do que as ondas incidentes. Quando a luz incidente é de cor azul, essa mudança resulta em elétrons muito mais rápidos. A razão é que a luz pode se comportar não apenas como ondas contínuas, mas também como feixes discretos de energia chamados de fótons. Um fóton azul, por exemplo, contém mais energia do que um fóton vermelho. Assim, o fóton azul age essencialmente como uma "bola de bilhar" com mais energia, desta forma transmitindo maior movimento a um elétron. Esta interpretação corpuscular da luz também explica por que a maior intensidade aumenta o número de elétrons ejetados - com mais fótons colidindo no metal, mais elétrons têm probabilidade de serem atingidos. Aumentar a intensidade de radiação que provoca o efeito fotoelétrico não aumenta a velocidade dos fotoelétrons, mas aumenta o número de fotoelétrons. Para se aumentar a velocidade dos fotoelétrons, é necessário excitar a placa com radiações de frequências maiores e, portanto, energias mais elevadas.[1] Equações Analisando o efeito fotoelétrico quantitativamente usando o método de Einstein, as seguintes equações equivalentes são usadas: Energia do fóton = Energia necessária para remover um elétron + Energia cinética do elétron emitido Mais detalhes em: Energia do fóton Algebricamente: ${\displaystyle hf=\phi +E_{c_{max}}\,}$ /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. Onde: h é a constante de Planck, f é a frequência do foton incidente, ${\displaystyle \phi =hf_{0}\ }$ é a função trabalho, ou energia mínima exigida para remover um elétron de sua ligação atômica, ${\displaystyle E_{c_{max}}={\frac {1}{2}}mv_{m}^{2}}$  /////// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL. é a energia cinética máxima dos elétrons expelidos, f0 é a frequência mínima para o efeito fotoelétrico ocorrer, m é a massa de repouso do elétron expelido, e vm é a velocidade dos elétrons expelidos. Notas: Se a energia do fóton (hf) não é maior que a função trabalho (${\displaystyle \phi }$), nenhum elétron será emitido. A função trabalho é ocasionalmente designada por ${\displaystyle W}$. Em física do estado sólido costuma-se usar a energia de Fermi e não a energia de nível de vácuo como referencial nesta equação, o que faz com que a mesma adquira uma forma um pouco diferente. Note-se ainda que ao aumentar a intensidade da radiação incidente não vai causar uma maior energia cinética dos elétrons (ou electrões) ejectados, mas sim um maior número de partículas deste tipo removidas por unidade de tempo.